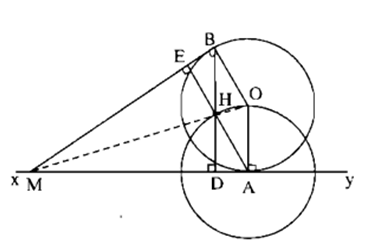
Cho đường tròn (O) và điểm A cố định trên đường tròn. Gọi xy là tiếp tuyến với đường tròn tại A. Từ một điểm M nằm trên xy, vẽ tiếp tuyến MB với đường tròn. Gọi H là trực tâm của tam giác MAB. Chứng minh rằng ba điểm M, H, O thẳng hàng.
Câu hỏi trong đề: Giải Sách Bài Tập Toán 9 Tập 1 !!
Quảng cáo
Trả lời:
Gọi BD, AE là đường cao của MAB. Ta có ΔMAE = MBD (cạnh huyền – góc nhọn) nên ME = MD, MHE = MHD (cạnh huyền – cạnh góc vuông) nên (EMH) = (DMH). MH và MO đều là tia phân giác của góc AMB nên M, H, O thẳng hàng.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Tam giác EBM cân nên . Suy ra , tức là ME ⊥ OM tại M. Vậy ME là tiếp tuyến của nửa đường tròn.
Lời giải
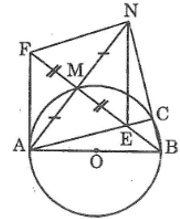
Tam giác ABM nội tiếp trong đường tròn (O) có AB là đường kính nên vuông tại M
Suy ra: AN ⊥ BM
Tam giác ABC nội tiếp trong đường tròn (O) có AB là đường kính nên vuông tại C
Suy ra: AC ⊥ BN
Tam giác ABN có hai đường cao AC và BM cắt nhau tại E nên E là trực tâm của tam giác ABN
Suy ra: NE ⊥ AB
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.