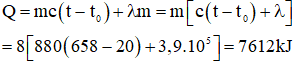Một đám mây thể tích 2,0. chứa hơi nước bão hòa trong khí quyển ở nhiệt độ 20C. Khi nhiệt độ của đám mây giảm xuống tới 10C, hơi nước bão hòa trong đám mây tụ lại thành các hạt mưa. Xác định khối lượng nước mưa rơi xuống. Cho biết khối lượng riêng của hơi nước bão hòa trong không khí ở 10C là 9,40 g/ và ở 20C là 17,30 g/
Câu hỏi trong đề: Giải Sách Bài Tập Vật Lí 10 Phần 2: Nhiệt học !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Vì độ ẩm cực đại của không khí ở 20C có giá trị bằng khối lượng riêng của hơi nước bão hoà ở cùng nhiệt độ, nên ta có : = 17,30 g/
và suy ra lượng hơi nước cực đại có trong thể tích V = 2,0. của đám mây :
= V = 17,30..2,0. = 3,46. kg
Khi nhiệt độ không khí của đám mây giảm xuống tới 10C thì lượng hơi nước cực đại có trong thể tích V = 2,0. của đám mây chỉ còn bằng :
= V = 9,40..2,0. = l,88. kg. Như vậy khối lượng nước mưa rơi xuống bằng :
M = - = 3,46.- l,88. = 1,58. kg = 158. tấn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Chọn đáp án B
Lượng nhiệt Q cung cấp để làm nóng chảy hoàn toàn thỏi nhôm khối lượng m = 8kg ở = 20°C có giá trị bằng:
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Lượng nhiệt cần cung cấp để biến đổi m = 6,0 kg nước đá ở nhiệt độ = -20C biến thành hơi nước ở = 100C có giá trị bằng :
Q =
trong đó lượng nhiệt = m( - ) cung cấp cho m (kg) nước đá có nhiệt dung riêng để nhiệt độ của nó tăng từ = -20C đến = 0C ; lượng nhiệt = m cung cấp cho m (kg) nước đá có nhiệt nóng chảy riêng ở = 0C tan thành nước ở cùng nhiệt độ ; lượng nhiệt = m( -)
cung cấp cho m (kg) nước có nhiệt dung riêng để nhiệt độ của nó tăng từ = 0C đến = 100C ; lượng nhiệt = Lm cung cấp cho m (kg) nước có nhiệt hoá hơi riêng L ở = 100C biến thành hơi nước ở cùng nhiệt độ. Như vậy, ta có thể viết:
Q = m( - ) + m + m( -) + Lm
hay Q = m[( - ) + + ( -) + L]
Thay số, ta tìm được :
Q = 6,0. [2090.(0 + 20) + 3,4. + 4180.(100 - 0) + 2,3.]
Q ≈ 186. J.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập