Câu hỏi trong đề: Giải bài tập SGK Toán 9 tập 2 hay nhất Bài tập ôn cuối năm !!
Quảng cáo
Trả lời:
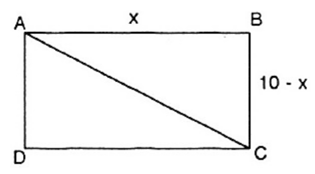
Gọi độ dài một cạnh của hình chữ nhật là x (x > 0, cm)
Nửa chu vi hình chữ nhật là: 20 : 2 = 10 (cm)
Độ dài cạnh còn lại của hình chữ nhật là : 10 – x (cm).
Theo định lý Pytago ta có:
⇒ AC ≥ 5√2
Dấu "=" xảy ra khi = 0 ⇔ x = 5.
Vậy đường chéo AC nhỏ nhất là 5√2cm khi ABCD là hình vuông cạnh bằng 5cm.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi số sách ở giá thứ nhất là x ( cuốn)
Số sách ở giá thứ hai là y (cuốn), (x, y∈ N*; x> 50, x< 450, y< 450)
Hai giá sách có tất cả 450 cuốn nên x+ y = 450 (1)
Khi chuyển 50 cuốn từ giá thứ nhất sang giá thứ hai thì số sách ở giá thứ nhất khi đó là x- 50 và số sách ở giá thứ hai là y+ 50
Theo đầu bài ta có:
Vậy số sách ở giá thứ nhất là 300 quyển, giá thứ hai là 150 quyển.
Lời giải
Gọi số đo độ dài hai cạnh góc vuông của tam giác vuông đó là x(cm), y (cm)
( 0 < y < x < 10)
Hai cạnh góc vuông có độ dài hơn kém nhau 2cm nên ta được x – y = 2 , (1).
Theo định lý Pytago ta có:
Từ (1) và (2) ta có hệ phương trình:
Từ (1) suy ra: x= y+ 2 thay vào (2) ta được:
Giải ra ta được: 0 ( loại)
Với y= 6 suy ra x = 8.
Vậy độ dài các cạnh góc vuông của tam giác vuông là 6cm và 8cm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

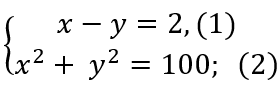
 ΔOED. Từ đó suy ra tia DO là tia phân giác của góc BDE.
ΔOED. Từ đó suy ra tia DO là tia phân giác của góc BDE.