Câu hỏi:
13/07/2024 2,746Lớp 6A có 15 học sinh thích môn Ngữ văn, 20 học sinh thích môn Toán. Trong số các học sinh thích môn Ngữ văn hoặc môn Toán có 8 học sinh thích cả hai môn Toán và Ngữ văn. Ngoài ra, trong lớp vẫn còn có 10 học sinh không thích môn nào (trong cả hai môn Ngữ văn và Toán). Lớp 6A có tất cả bao nhiêu học sinh?
Câu hỏi trong đề: Giải SBT Toán 6 Chương 1: Số tự nhiên - Bộ Cánh diều !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
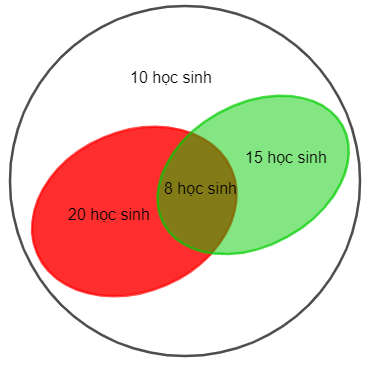
Số học sinh yêu thích riêng môn Ngữ văn là: 15 – 8 = 7 (học sinh).
Số học sinh yêu thích riêng môn Toán là: 20 – 8 = 12 (học sinh).
Tổng số học sinh yêu thích môn Ngữ văn và Toán là: 12 + 7 + 8 = 27 (học sinh).
Số học sinh của lớp 6A là: 27 + 10 = 37 (học sinh).
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Ta nhận thấy các phần tử của tập hợp A là các số tự nhiên lẻ lớn hơn 12 và nhỏ hơn 30.
Theo cách chỉ ra tính chất đặc trưng, ta viết:
A = {x | x là số tự nhiên lẻ, 12 < x < 30}.
b) Ta nhận thấy các phần tử của tập hợp B là các số tự nhiên chẵn lớn hơn hoặc bằng 22 và nhỏ hơn hoặc bằng 42.
Theo cách chỉ ra tính chất đặc trưng, ta viết:
B = {x|x là số tự nhiên chẵn, 22 ≤ x ≤ 42}.
c)
+) Cách 1:
Ta có:
7 = 4.1 + 3; 11 = 4.2 + 3; 15 = 4.3 + 3; 19 = 4.4 + 3; 23 = 4.5 + 3; 27 = 4.6 + 3.
Ta nhận thấy các số trên đều có dạng 4.x + 3 với x ∈ {1,2,3,4,5,6} .
Theo cách chỉ ra tính chất đặc trưng, ta viết:
C = {4x + 3| x là số tự nhiên, 0 < x < 7}.
+) Cách 2:
Ta nhận thấy các phần tử trong tập hợp C là các số tự nhiên lẻ và cách nhau 4 đơn vị.
C = {xk| xk là số tự nhiên lẻ, xk+1 – xk = 4,k ∈ N }.
d) Ta thấy các phần tử của tập hợp D là các số chính phương lớn hơn 3 và nhỏ hơn 50.
Theo cách chỉ ra tính chất đặc trưng, ta viết:
D = {x| x là số chính phương, 3 < x < 50}.
Lời giải
Các năng lượng tái tạo trên thế giới: năng lượng gió; năng lượng Mặt trời, năng lượng địa nhiệt.
Khi đó tập X = {năng lượng gió; năng lượng Mặt trời; năng lượng địa nhiệt}.
Các năng lượng tái tạo mà Việt Nam sản xuất: năng lượng gió; năng lượng Mặt trời.
Khi đó tập Y = {năng lượng gió; năng lượng Mặt trời}.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Đề thi Cuối học kì 2 Toán 6 có đáp án (Đề 1)
-
31 câu Trắc nghiệm Toán 6 Kết nối tri thức Bài 1: Tập hợp có đáp án
-
Dạng 4: Một số bài tập nâng cao về lũy thừa
-
Đề kiểm tra Giữa kì 2 Toán 6 có đáp án (Mới nhất) - Đề 1
-
10 câu Trắc nghiệm Toán 6 Chân trời sáng tạo Bài 1: Tập hợp. Phần tử của tập hợp (có đáp án)
-
Dạng 4: Trung điểm của đoạn thẳng có đáp án
-
Dạng 6: Bài tập vận dụng có đáp án
-
Đề kiểm tra Giữa kì 2 Toán 6 có đáp án (Mới nhất) - Đề 11