Một người chạy tập thể dục trên một con đường hình vuông khép kín có chu vi 400 m. Bên trong vùng đất được bao bởi con đường có đặt một nguồn âm điểm phát âm đẳng hướng ra bên ngoài. Khi đi hết một vòng khép kín thì người đó thấy có hai vị trí mà mức cường độ âm bằng nhau và là lớn nhất có giá trị \({L_1}\) và có một điểm duy nhất mức cường độ âm nhỏ nhất là \({L_2}\) trong đó \[{L_1} = {L_2} + 10\]dB. Khoảng cách từ nguồn âm đến tâm của hình vuông tạo bởi con đường gần nhất với giá trị nào sau đây?
Quảng cáo
Trả lời:
Phương pháp:
Khái niệm cường độ điện hiệu dụng được xây dựng dựa vào tác dụng nhiệt của dòng điện.
Cách giải:
Giả sử nguồn âm đặt tại O, cách tâm hình vuông đoạn d
Hình vuông có chu vi 400m nên mỗi cạnh có chiều dài 100m
Vì có hai vị trí có cường độ âm lớn nhất và bằng nhau nên OA = OB và mức cường độ âm lớn nhất đo được tại A và B, mức cường độ âm nhỏ nhất đo được tại C
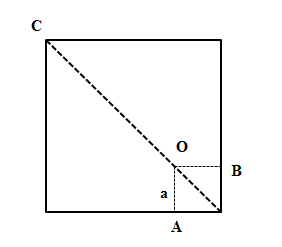
Ta có: \[{I_A} = {I_B} = \frac{P}{{4\pi {a^2}}} = {I_0}{.10^{\frac{{{L_1}}}{{10}}}}\] (1)
(2)
Vì L1=L2+10(dB) \[ \Rightarrow \frac{{{L_1}}}{{10}} = \frac{{{L_2}}}{{10}} + 1 \Rightarrow {10^{\frac{{{L_1}}}{{10}}}} = {10^{\frac{{{L_2}}}{{10}}}}.10\] (3)
Từ (1,2,3) ta có:
Vậy khoảng cách từ O đến tâm hình vuông là
Chọn B.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 500 Bài tập tổng ôn Vật lí (Form 2025) ( 38.000₫ )
- 1000 câu hỏi lí thuyết môn Vật lí (Form 2025) ( 45.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Phương pháp:
Cường độ dòng điện ở cuộn thứ cấp:\[I = \frac{P}{U}\]
⇒Điện áp ở cuối đường dây:\[U' = U - I.R\]
Cách giải:
Dòng điện ở cuộn thứ cấp là: \[I = \frac{P}{U} = \frac{{{{4.10}^3}}}{{220}} = \frac{{200}}{{11}}A\]
⇒Điện áp ở cuối đường dây: \[U' = U - I.R = 220 - \frac{{200}}{{11}}.2 = 183,6V\]
Chọn A.
Lời giải
Phương pháp:
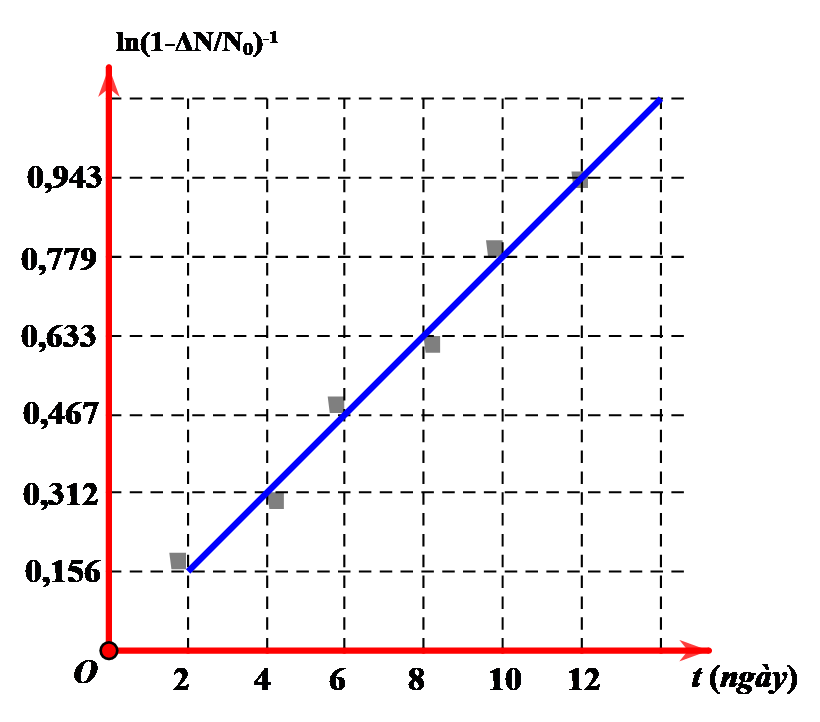
\[{\rm{\Delta }}N = {N_0}\left( {1 - {2^{ - \frac{t}{T}}}} \right)\]
Cách giải:
Ta có: \[{\left( {1 - \frac{{{\rm{\Delta }}N}}{{{N_0}}}} \right)^{ - 1}} = \frac{1}{{1 - \frac{{{\rm{\Delta }}N}}{{{N_0}}}}} = \frac{1}{{1 - \left( {1 - {2^{ - \frac{t}{T}}}} \right)}} = \frac{1}{{{2^{ - \frac{t}{T}}}}} = {2^{\frac{t}{T}}}\]
\[ \Rightarrow ln{(1 - \frac{{\Delta N}}{{{N_0}}})^{ - 1}} = ln{2^{\frac{t}{T}}}\]
Từ đồ thị ta thấy: t=6 ngày
\[\ln {(1 - \frac{{\Delta N}}{{{N_0}}})^{ - 1}} = 0,467 \Rightarrow ln{2^{\frac{6}{T}}} = 0,467 \Rightarrow T = 8,82\]ngày
Chọn A.Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.