Trong mạch dao động \[LC\] lí tưởng, hệ số tự cảm \[L\] và điện dung \[C\]. Tốc độ truyền ánh sáng trong chân không là \[c\]. Bước sóng mà mạch này có thể phát ra được tính theo công thức

Phương pháp: 

Cường độ dòng điện ở cuộn thứ cấp:\[I = \frac{P}{U}\]

⇒Điện áp ở cuối đường dây:\[U' = U - I.R\]

Cách giải: 

Dòng điện ở cuộn thứ cấp là: \[I = \frac{P}{U} = \frac{{{{4.10}^3}}}{{220}} = \frac{{200}}{{11}}A\]

⇒Điện áp ở cuối đường dây: \[U' = U - I.R = 220 - \frac{{200}}{{11}}.2 = 183,6V\]

Chọn A.

Phương pháp: 

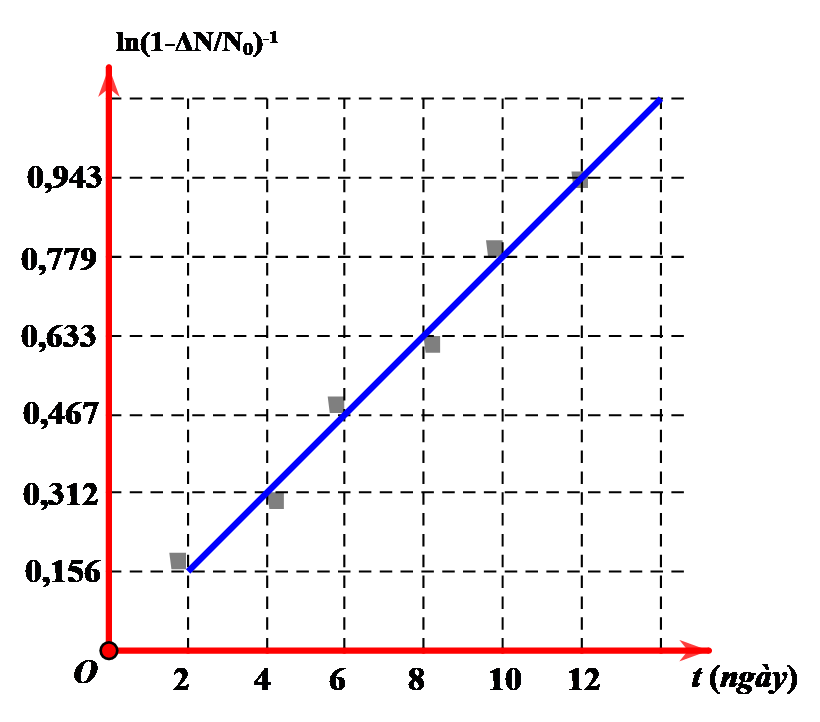
\[{\rm{\Delta }}N = {N_0}\left( {1 - {2^{ - \frac{t}{T}}}} \right)\]

Cách giải: 

Ta có: \[{\left( {1 - \frac{{{\rm{\Delta }}N}}{{{N_0}}}} \right)^{ - 1}} = \frac{1}{{1 - \frac{{{\rm{\Delta }}N}}{{{N_0}}}}} = \frac{1}{{1 - \left( {1 - {2^{ - \frac{t}{T}}}} \right)}} = \frac{1}{{{2^{ - \frac{t}{T}}}}} = {2^{\frac{t}{T}}}\]

\[ \Rightarrow ln{(1 - \frac{{\Delta N}}{{{N_0}}})^{ - 1}} = ln{2^{\frac{t}{T}}}\]

Từ đồ thị ta thấy: t=6 ngày

\[\ln {(1 - \frac{{\Delta N}}{{{N_0}}})^{ - 1}} = 0,467 \Rightarrow ln{2^{\frac{6}{T}}} = 0,467 \Rightarrow T = 8,82\]ngày