Một sợi dây đàn hồi có một đầu cố định, một đầu tự do. Thay đổi tần số dao động của sợi dây thì thấy trên dây có sóng dừng với hai tần số liên tiếp là 30Hz và 50Hz. Tần số nhỏ nhất để có sóng dừng trên dây là
Quảng cáo
Trả lời:
Phương pháp:
Điều kiện có sóng dừng trên dây 1 đầu cố định – 1 đầu tự do: \(l = \left( {k + \frac{1}{2}} \right)\frac{\lambda }{4}\)
Cách giải:
Trên sợi dây đàn hồi có một đầu cố định, một đầu tự do có sóng dừng: \(l = \left( {k + \frac{1}{2}} \right)\frac{\lambda }{4} = \left( {k + \frac{1}{2}} \right)\frac{v}{{2f}}\)
Khi \({f_1} = 30\;{\rm{Hz}}:l = \left( {{k_1} + \frac{1}{2}} \right)\frac{v}{{2{f_1}}}\left( 1 \right)\)
Khi \({f_2} = 50\;{\rm{Hz}}:l = \left( {{k_2} + \frac{1}{2}} \right)\frac{v}{{2{f_2}}} = \left[ {\left( {{k_1} + 1} \right) + \frac{1}{2}} \right]\frac{v}{{2{f_2}}}\left( 2 \right)\)
Lấy \(\frac{{\left( 1 \right)}}{{\left( 2 \right)}}\) ta được: \(1 = \frac{{{k_1} + \frac{1}{2}}}{{{k_1} + \frac{3}{2}}} \cdot \frac{{{f_2}}}{{{f_1}}} \Leftrightarrow 1 = \frac{{{k_1} + \frac{1}{2}}}{{{k_1} + \frac{3}{2}}} \cdot \frac{5}{3} \Rightarrow {k_1} = 1\)
Thay vào (1) suy ra: \(\frac{v}{l} = \frac{{2{f_1}}}{{1,5}} = 40\)
Tần số nhỏ nhất để có sóng dừng trên dây: \({f_0} = \frac{v}{{4l}} = \frac{{40}}{4} = 10\;{\rm{Hz}}\)
Chọn B.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 500 Bài tập tổng ôn Vật lí (Form 2025) ( 38.000₫ )
- 1000 câu hỏi lí thuyết môn Vật lí (Form 2025) ( 45.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. sớm pha hơn một góc \(\frac{\pi }{2}\)
Lời giải
Phương pháp:
Đoạn mạch xoay chiều chỉ có tụ điện:
Cách giải:
Mạch chỉ có tụ điện khi đó: u trễ pha hơn i một góc \(\frac{\pi }{2}\) hay nói cách khác i nhanh pha hơn u một góc \(\frac{\pi }{2}\).
Chọn C.
Lời giải
Phương pháp:
Sử dụng biểu thức định luật khúc xạ ánh sáng: \({n_1}\sin i = {n_2}{\rm{ sinr }}\)
Cách giải:
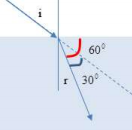
Theo bài ra ta có hình vẽ:
Góc khúc xạ: \(r = {90^0} - {60^0} = {30^0}\)
Góc tới: \(i = r + {30^0} = {30^0} + {30^0} = {60^0}\)
Áp dụng định luật khúc xạ ánh sáng ta có:
Chọn A.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.