Trong thí nghiệm Y-âng về giao thoa ánh sáng, màn quan sát E cách mặt phẳng chứa hai khe 1 2 SSmột khoảng 1,2m. Đặt giữa mặt phẳng hai khe một thấu kính hội tụ, người ta tìm được 2 vị trí của thấu kính cách nhau 72cm cho ảnh rõ nét của hai khe trên màn, ở vị trí ảnh lớn hơn thì khoảng cách giữa hai khe ảnh là 4mm. Bỏ thấu kính đi, rồi chiếu sáng hai khe bằng nguồn điểm S phát bức xạ đơn sắc 750nm thì khoảng vân thu được trên màn là
A. 3,6 mm.
Quảng cáo
Trả lời:
Phương pháp:
+ Sử dụng công thức thấu kính: \(\frac{1}{f} = \frac{1}{d} + \frac{1}{{{d^\prime }}}\)
+ Sử dụng công thức viét: \(\left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} = S}\\{{x_1} \cdot {x_2} = P}\end{array} \Rightarrow {X^2} - SX + P = 0} \right.\)
+ Sử dụng công thức tính khoảng vân: \(i = \frac{{\lambda D}}{a}\)
Cách giải:
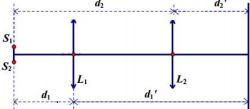
Trên hình vẽ, ta có \({L_1};{L_2}\) là 2 vị trí của thấu kính sao cho ảnh rõ nét của 2 nguồn trên màn.
Gọi f là tiêu ực của thấu kính, ta có:
+ Xét vị trí \({L_1}:\frac{1}{f} = \frac{1}{{{d_1}}} + \frac{1}{{d_1^\prime }}\)
+ Xét vị trí \({L_2}:\frac{1}{f} = \frac{1}{{{d_2}}} + \frac{1}{{d_2^\prime }} \Rightarrow \frac{1}{{{d_1}}} + \frac{1}{{d_1^\prime }} = \frac{1}{{{d_2}}} + \frac{1}{{d_2^\prime }}\)
Lại có: (1)
Từ (1) ta suy ra \({d_1};{d_1}^\prime \) là 2 nghiệm của phương trình: \({X^2} - S{\rm{X}} + P = 0\) và \({d_2};{d_2}'\) cũng vậy.
Phương trình trên là phương trình bậc 2 chó 2 nghiệm phân biệt \({X_1},{X_2}\)
Do \({d_1} \ne {d_2}\) nên
Theo đề bài ta có:
Ta xét 1 vị trí bất kì của thấu kính
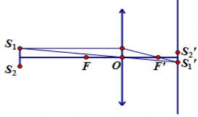
Từ hình vẽ, ta có:
Suy ra để có ảnh lớn hơn, ta phải có \(\frac{{{d^\prime }}}{d} > 1\). Tức là thấu kính gần \({S_1}{S_2}\) hơn
Khi đó:
Vậy \(a = 1\;{\rm{mm}}\)
Khi bỏ thấu kính cho giao thoa ánh sáng trên màn khi đó có khoảng vân:
Chọn D.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 500 Bài tập tổng ôn Vật lí (Form 2025) ( 38.000₫ )
- 1000 câu hỏi lí thuyết môn Vật lí (Form 2025) ( 45.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. sớm pha hơn một góc \(\frac{\pi }{2}\)
Lời giải
Phương pháp:
Đoạn mạch xoay chiều chỉ có tụ điện:
Cách giải:
Mạch chỉ có tụ điện khi đó: u trễ pha hơn i một góc \(\frac{\pi }{2}\) hay nói cách khác i nhanh pha hơn u một góc \(\frac{\pi }{2}\).
Chọn C.
Lời giải
Phương pháp:
Sử dụng biểu thức định luật khúc xạ ánh sáng: \({n_1}\sin i = {n_2}{\rm{ sinr }}\)
Cách giải:
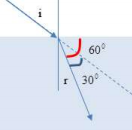
Theo bài ra ta có hình vẽ:
Góc khúc xạ: \(r = {90^0} - {60^0} = {30^0}\)
Góc tới: \(i = r + {30^0} = {30^0} + {30^0} = {60^0}\)
Áp dụng định luật khúc xạ ánh sáng ta có:
Chọn A.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.