Câu hỏi:
13/07/2024 768
Chùa Một Cột (hình 13.15) là một vật có tính đối xứng gương, tức là có thể chia vật thành hai phần bằng nhau sao cho phần này giống như ảnh của phần kia qua một gương phẳng.
Sưu tầm các tranh, ảnh về các vật có tính đối xứng gương trong đời sống.
Chùa Một Cột (hình 13.15) là một vật có tính đối xứng gương, tức là có thể chia vật thành hai phần bằng nhau sao cho phần này giống như ảnh của phần kia qua một gương phẳng.
Sưu tầm các tranh, ảnh về các vật có tính đối xứng gương trong đời sống.
Câu hỏi trong đề: Giải SGK KHTN 7 Bài 13. Sự phản xạ ánh sáng có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
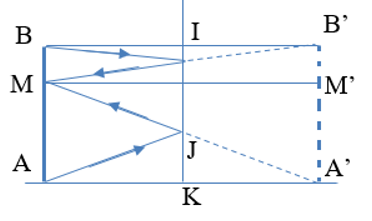
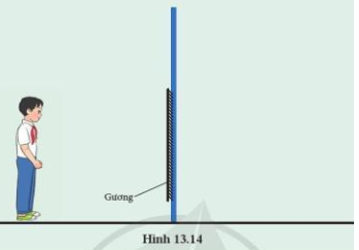
+ Gọi AB là chiều cao của bạn học sinh đó, M là điểm đặt mắt.
+ Khi đó A’B’ là ảnh của AB; M’ là ảnh của mắt (M).
+ Để mắt có thể nhìn thấy ảnh A’B’ qua gương thì từ AB phải có tia sáng truyền đến gương và cho tia phản xạ đến mắt. Khi đó nối M với B’; nối M với A’ cắt tường ở điểm I và J.
+ Vậy khi đó IJ là chiều cao tối thiểu của gương.
Lưu ý: Gương phải treo thẳng và mép dưới của gương phải cách mặt đất một khoảng là JK.
Sử dụng các tính chất trong hình học cho các hình chữ nhật AMM’A’ và MBB’M’.
Khi đó: hay .
Vậy chiều cao tối thiểu của gương là 0,8 m và treo cách mặt đất 0,76 m.
Lời giải
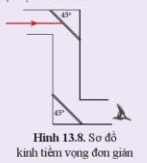
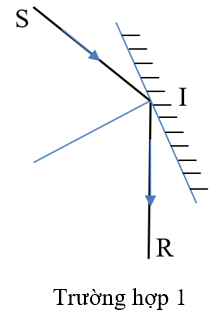
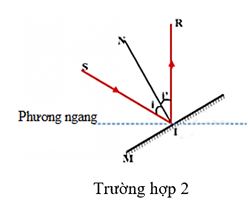
b. Nếu giữ nguyên tia tới SI, để có tia phản xạ hướng theo phương thẳng đứng thì phải xoay gương. Để xác định được vị trí xoay chính xác ta cần làm như sau:
+ Vẽ tia phản xạ có phương thẳng đứng hướng xuống hoặc hướng lên.
+ Xác định góc hợp bởi tia tới và tia phản xạ.
+ Theo định luật phản xạ ánh sáng thì góc tới và góc phản xạ bằng nhau, khi đó tia phân giác của góc hợp bởi tia tới và tia phản xạ chính là pháp tuyến.
+ Tiếp theo vẽ đường thẳng vuông góc với pháp tuyến. Đó chính là vị trí gương cần tìm, lưu ý mặt phản xạ gương cùng phía với các tia tới và pháp tuyến.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Đề kiểm tra giữa kì 2 Khoa học tự nhiên 7 KNTT (Song song) có đáp án - Đề 1
-
10 câu Trắc nghiệm Khoa học tự nhiên 7 Kết nối tri thức Bài 19 có đáp án
-
10 câu Trắc nghiệm Khoa học tự nhiên 7 Chân trời sáng tạo Bài 22 có đáp án
-
Đề kiểm tra giữa kì 2 Khoa học tự nhiên 7 KNTT (Song song) có đáp án - Đề 2
-
10 câu Trắc nghiệm Khoa học tự nhiên 7 Chân trời sáng tạo Bài 7 có đáp án
-
10 câu Trắc nghiệm Khoa học tự nhiên 7 Chân trời sáng tạo Bài 34 có đáp án
-
10 câu Trắc nghiệm Khoa học tự nhiên 7 Chân trời sáng tạo Bài 19 có đáp án
-
10 câu Trắc nghiệm Khoa học tự nhiên 7 Chân trời sáng tạo Bài 30 có đáp án