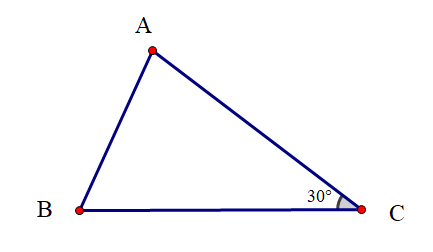
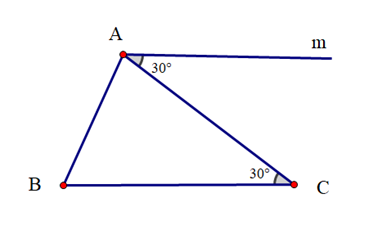
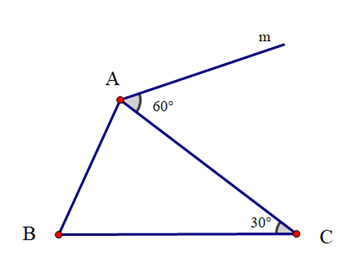
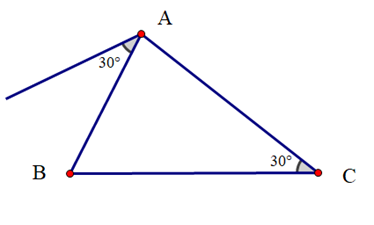
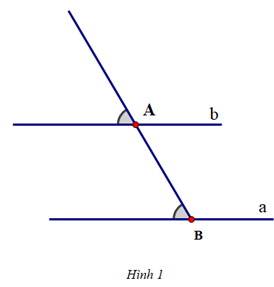
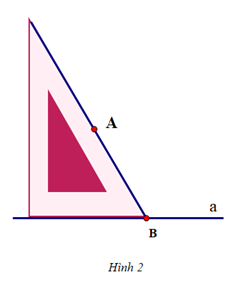
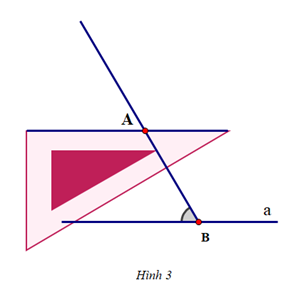
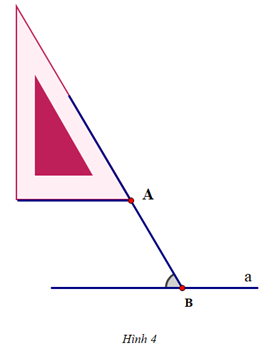
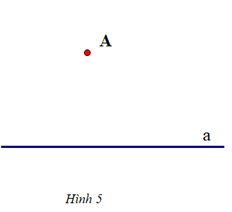
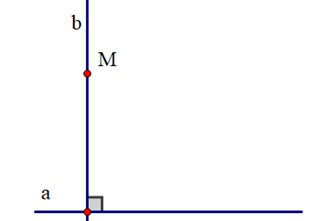
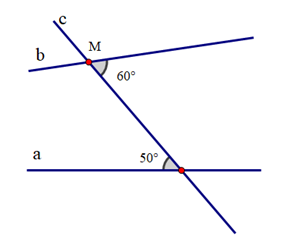
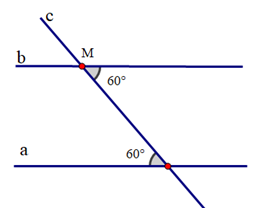
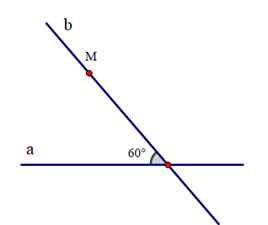
Vì sao khi sử dụng ê ke (góc 60°) ta có thể vẽ được đường thẳng đi qua một điểm và song song với đường thẳng cho trước?
A. Do hai đường thẳng phân biệt cùng cắt một đường thẳng thứ ba và tạo thành hai góc ở vị trí đồng vị bằng nhau;
B. Do hai đường thẳng cùng song song với một đường thẳng thứ ba nên chúng song song với nhau;
C. Do hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba nên chúng song song với nhau;
D. Do hai đường thẳng cắt nhau và tạo thành 1 cặp góc trong cùng phía bù nhau.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải:
Đáp án đúng là: A
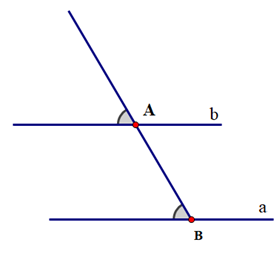
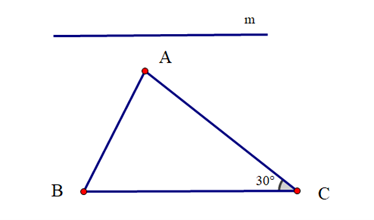
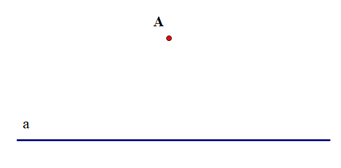
Khi vẽ đường thẳng đi qua một điểm và song song với một đường thẳng cho trước, ta có thể sử dụng ê ke (góc 60°) để vẽ vì nó sẽ tạo thành hai góc ở vị trí đồng vị bằng nhau (cùng bằng 60°) nên hai đường thẳng song song với nhau.
Hot: 1000+ Đề thi giữa kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. Hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba thì chúng song song với nhau;
B. Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau;
C. Hai đường thẳng phân biệt cùng đi qua một điểm thì chúng song song với nhau;
D. Một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng còn lại.
Lời giải
Hướng dẫn giải:
Đáp án đúng là: B
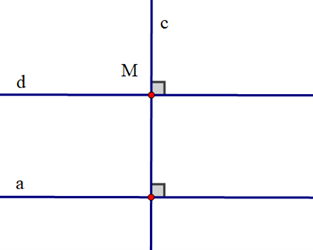
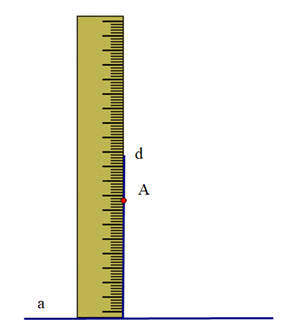
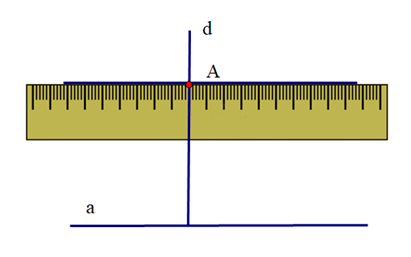
Vì hai đường thẳng a và d cùng vuông góc với đường thẳng c nên chúng song song với nhau. Do đó cách vẽ trên dựa vào tính chất: Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau.
.Lời giải
Hướng dẫn giải:
Đáp án đúng là: A
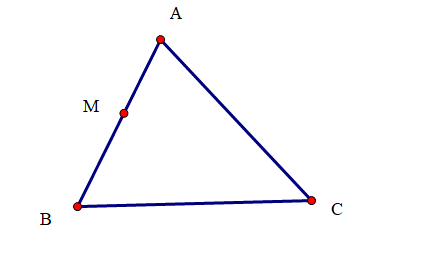
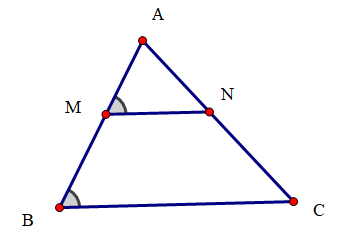
Hình A cho thấy đường thẳng MN đi qua M. Đường thẳng AC cắt hai đường thẳng BC, MN và tạo thành hai góc ở vị trí đồng vị bằng nhau nên MN song song với BC.
Câu 3
A. Hình 1 – Hình 2 – Hình 3;
B. Hình 2 – Hình 3 – Hình 1;
C. Hình 1 – Hình 3 – Hình 2;
D. Hình 2 – Hình 1 – Hình 3.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. Hình 5 – Hình 1 – Hình 2 – Hình 3 – Hình 4;
B. Hình 5 – Hình 2 – Hình 3 – Hình 4 – Hình 1;
C. Hình 5 – Hình 2 – Hình 4 – Hình 3 – Hình 1;
D. Hình 5 – Hình 2 – Hình 1 – Hình 3 – Hình 4.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo