Câu hỏi:
13/09/2022 453Cho \(\widehat {{\rm{DOF}}} = 140^\circ \), biết rằng OE là tia phân giác của \(\widehat {{\rm{DOF}}}\). Số đo của \(\widehat {EOF}\) là
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: C
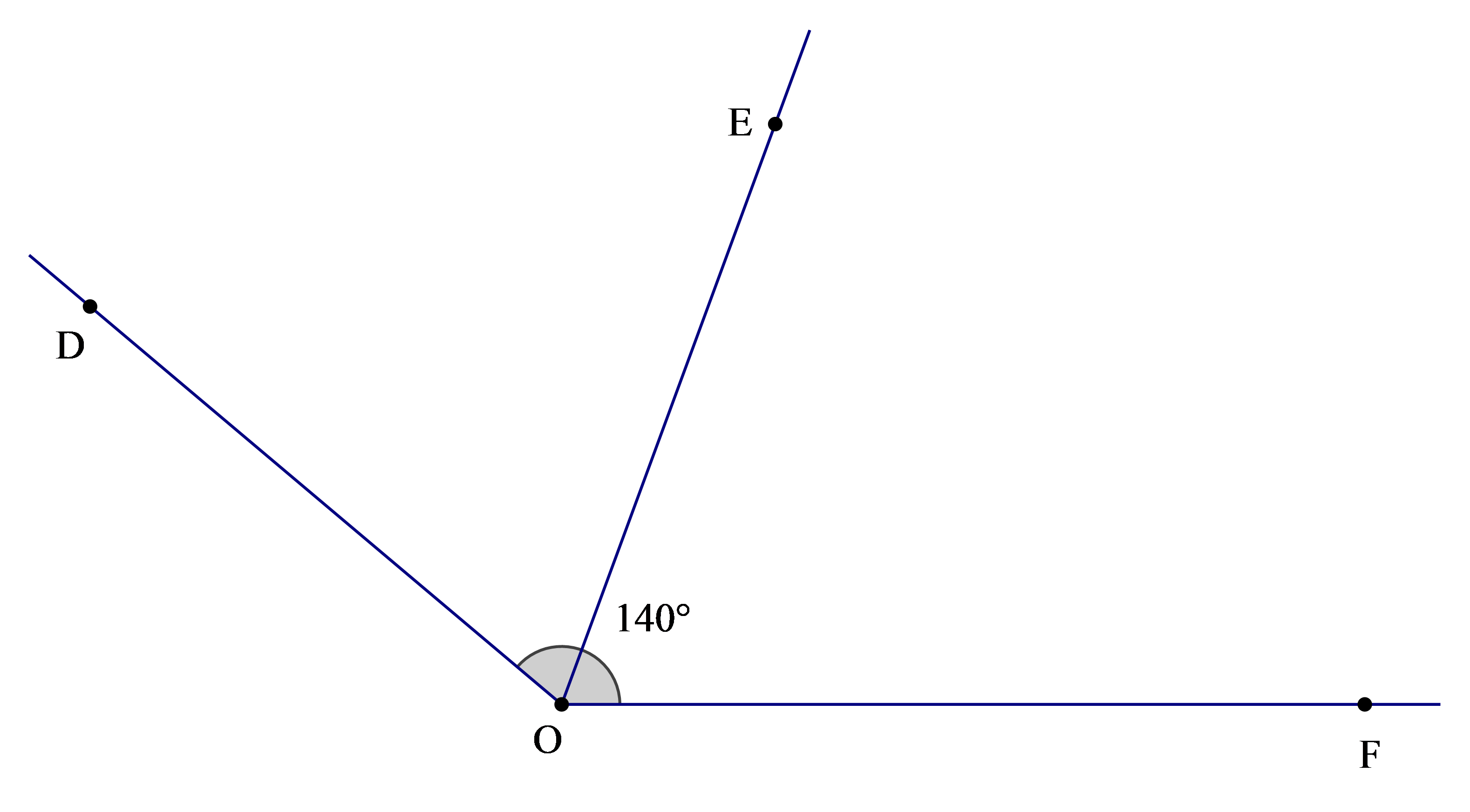
Theo bài ta có: OE là tia phân giác của \(\widehat {{\rm{DOF}}}\)
Nên \(\widehat {{\rm{DOE}}} = \widehat {EOF}\) (tính chất đường phân giác của một góc) (1)
Ta lại có \(\widehat {{\rm{DOE}}} + \widehat {EOF} = \widehat {{\rm{DOF}}}\) (hai góc kề nhau) (2)
Từ (1) và (2) suy ra \(\widehat {{\rm{DOE}}} = \widehat {EOF} = \frac{1}{2}\widehat {{\rm{DOF}}} = \frac{1}{2}.140^\circ = 70^\circ \)
Do đó \(\widehat {EOF} = 70^\circ \)
Vậy ta chọn phương án C.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
Đáp án đúng là: C
Hai góc kề nhau là hai góc có một cạnh chung và không có điểm trong chung.
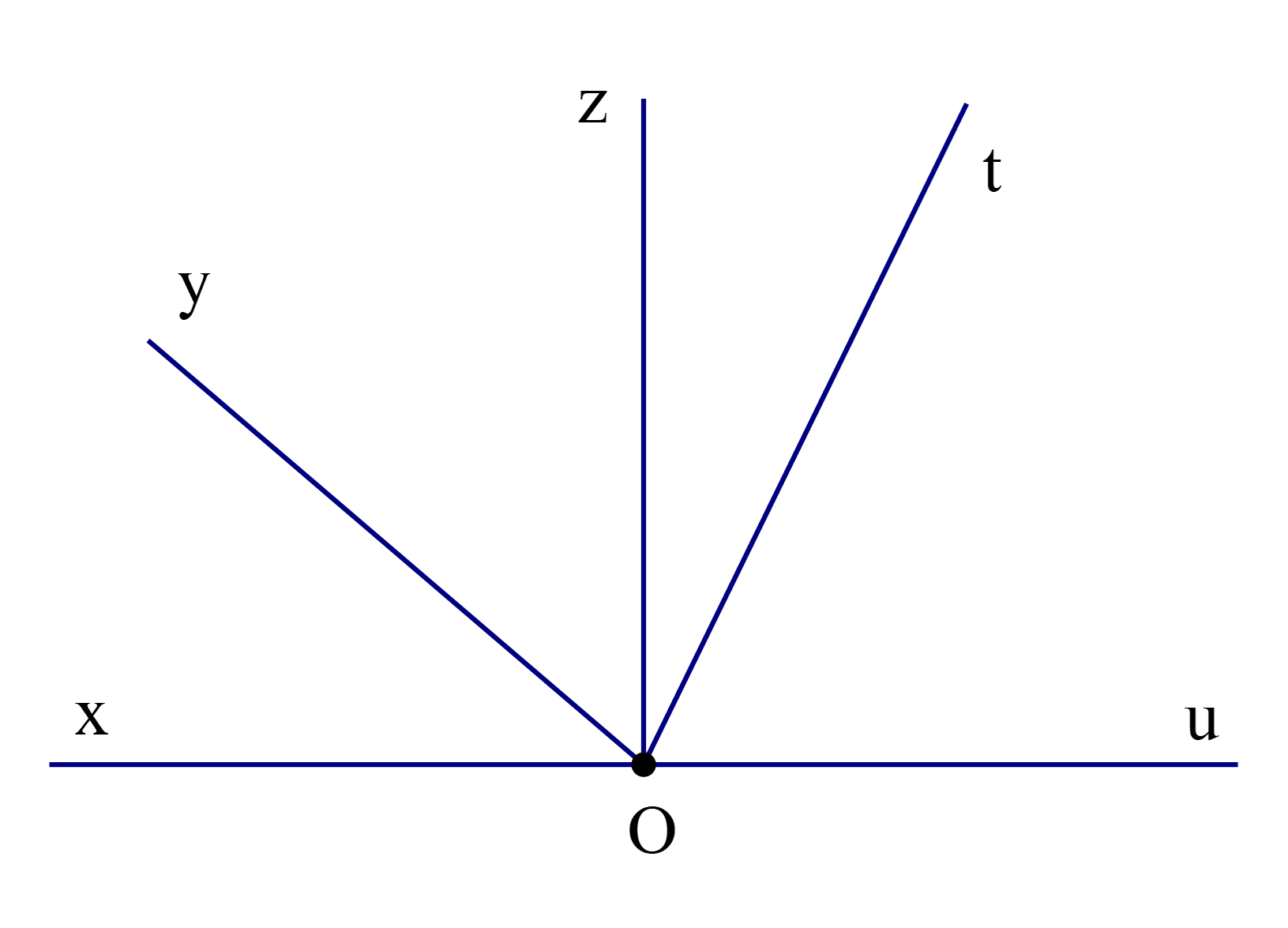
Do đó các góc kề với \(\widehat {{\rm{xOy}}}\)là: \(\widehat {{\rm{yOz}}}{\rm{; }}\widehat {{\rm{yOt}}}{\rm{; }}\widehat {{\rm{yOu}}}.\)
Vậy có tất cả 3 góc kề (không kể góc bẹt) với \(\widehat {{\rm{xOy}}}\).
Vậy ta chọn phương án C.
Lời giải
Hướng dẫn giải
Đáp án đúng là: B
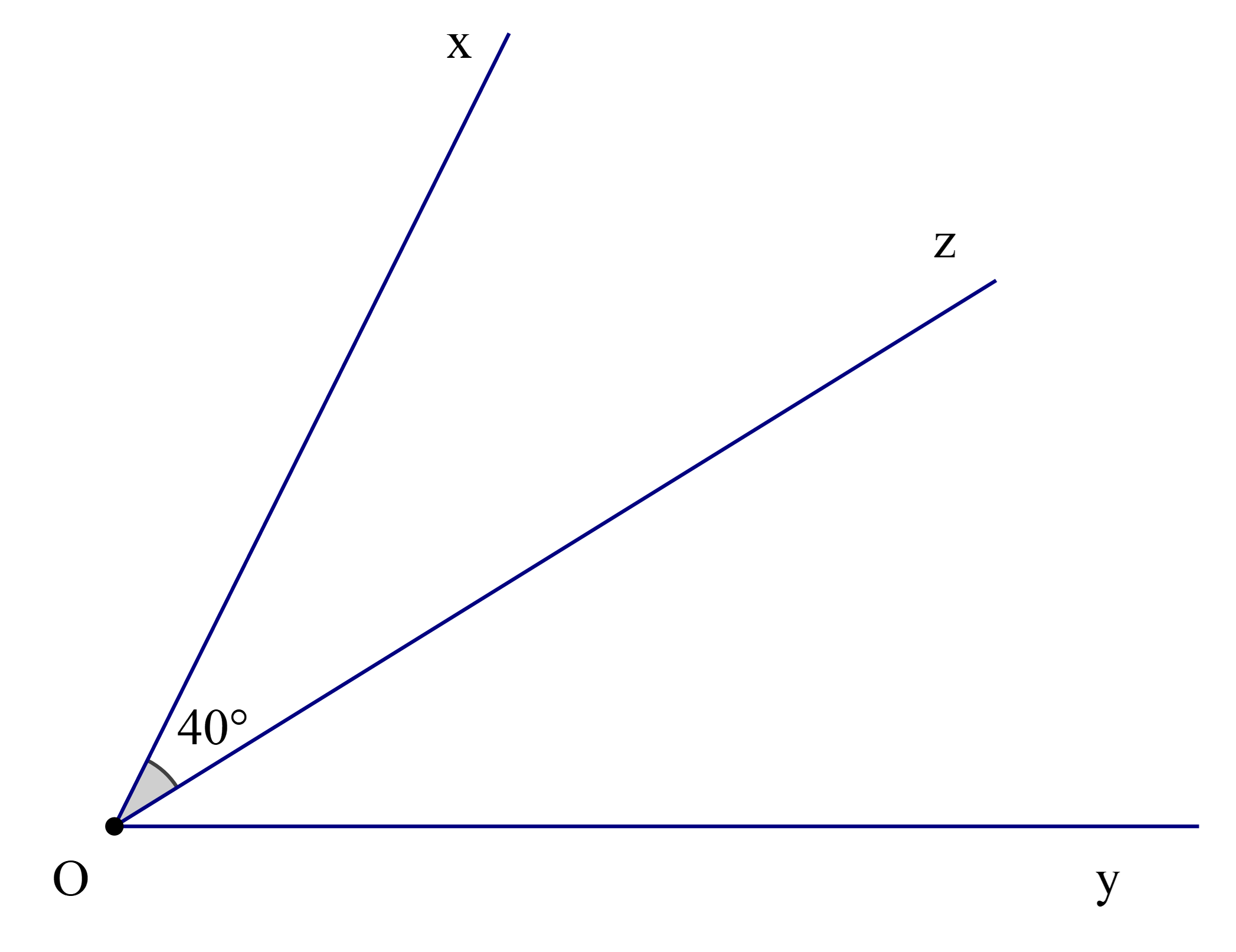
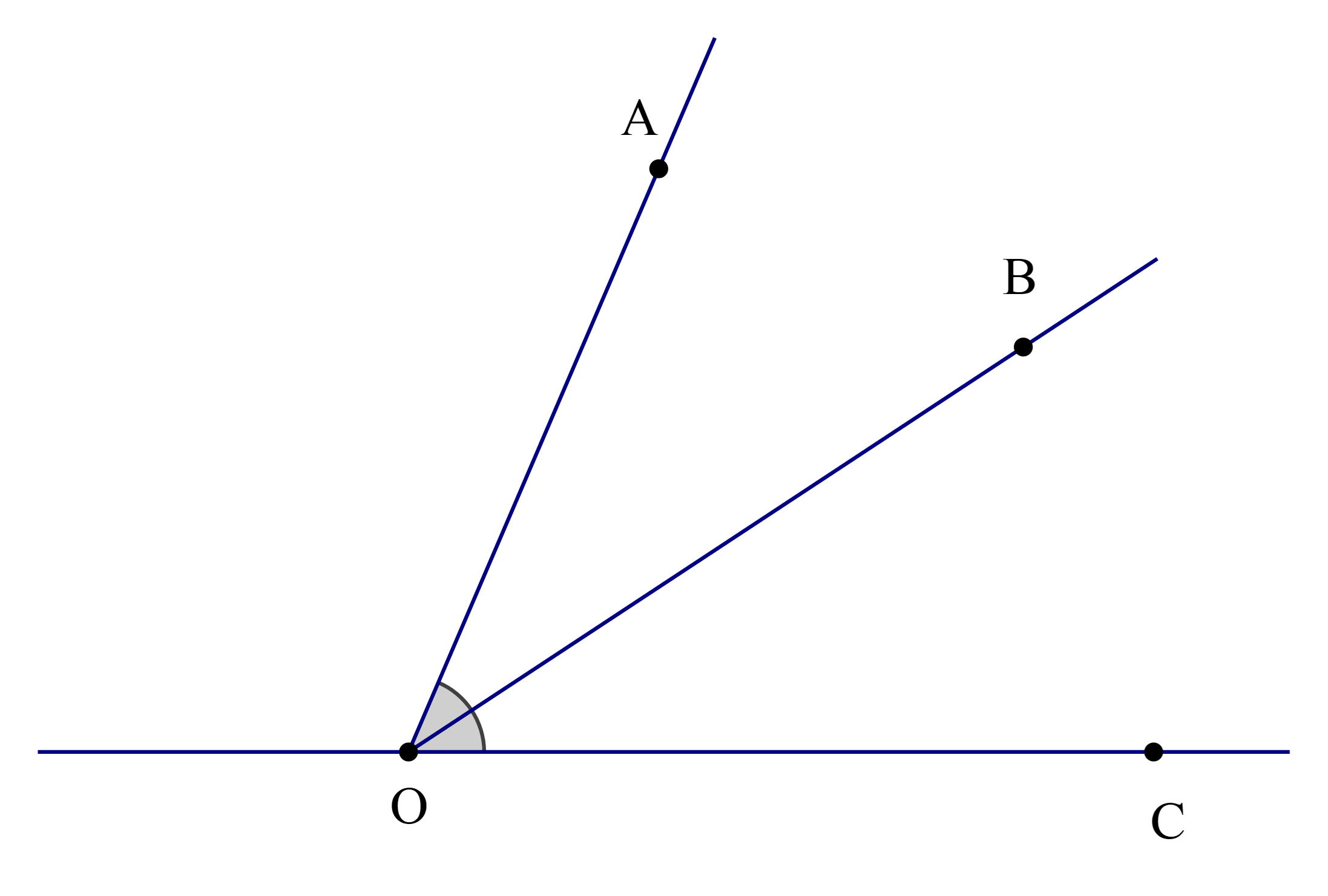
Theo bài ta có: Oz là tia phân giác của \(\widehat {{\rm{xOy}}}\)
Nên \(\widehat {{\rm{xOz}}} = \widehat {{\rm{zOy}}}\) (tính chất tia phân giác của một góc)
Mà \(\widehat {{\rm{xOz}}} = 40^\circ \)
Suy ra \(\widehat {{\rm{yOz}}} = 40^\circ \)
Vậy ta chọn phương án B.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 1
-
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 04
-
15 câu Trắc nghiệm Toán 7 Kết nối tri thức Bài 1: Tập hợp các số hữu tỉ có đáp án
-
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 2
-
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 01
-
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 02
-
Bộ 15 đề thi Học kì 2 Toán 7 có đáp án (Mới nhất) - đề 2
-
15 câu Trắc nghiệm Toán 7 Chân trời sáng tạo Bài 1: Tập hợp các số hữu tỉ có đáp án