Câu hỏi:
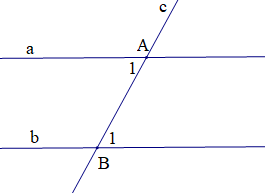
13/09/2022 428Cho hình vẽ. Biết rằng x // y; đường thẳng z cắt hai đường thẳng x, y lần lượt tại A, B sao cho \({\widehat {\rm{A}}_1} = 60^\circ \).
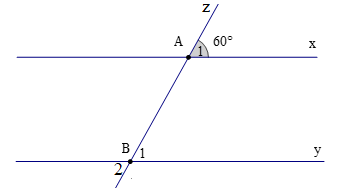
Số đó của \({\widehat {\rm{B}}_2}\) là:
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: A
Vì x // y nên \({\widehat {\rm{A}}_1}{\rm{ = }}{\widehat {\rm{B}}_1}{\rm{ = 60}}^\circ \) (hai góc đồng vị)
Ta có \({\widehat {\rm{B}}_1} = {\widehat {\rm{B}}_2}\) (hai góc đối đỉnh)
Suy ra \({\widehat {\rm{B}}_2} = 60^\circ \)
Vậy ta chọn phương án A.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
Đáp án đúng là: D
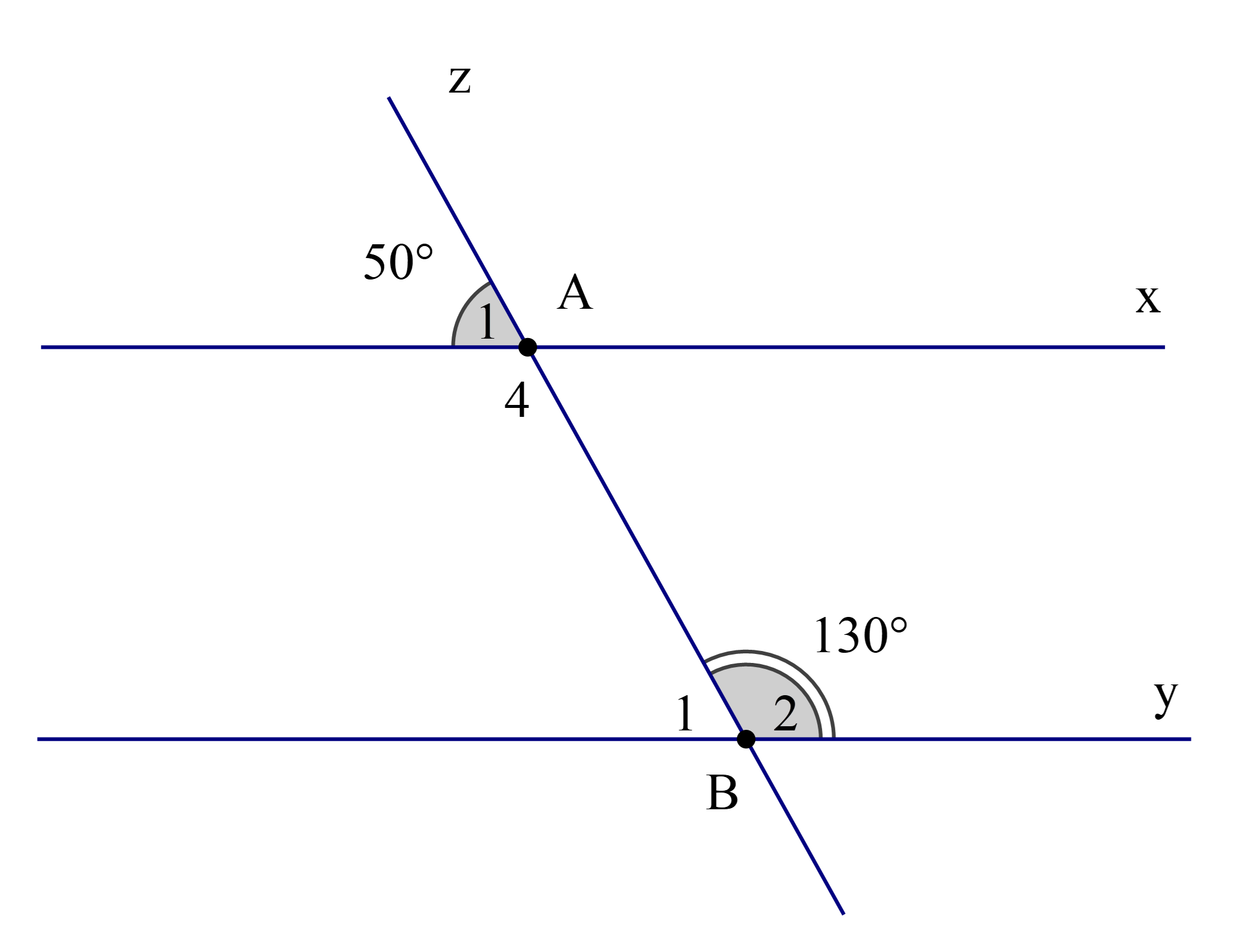
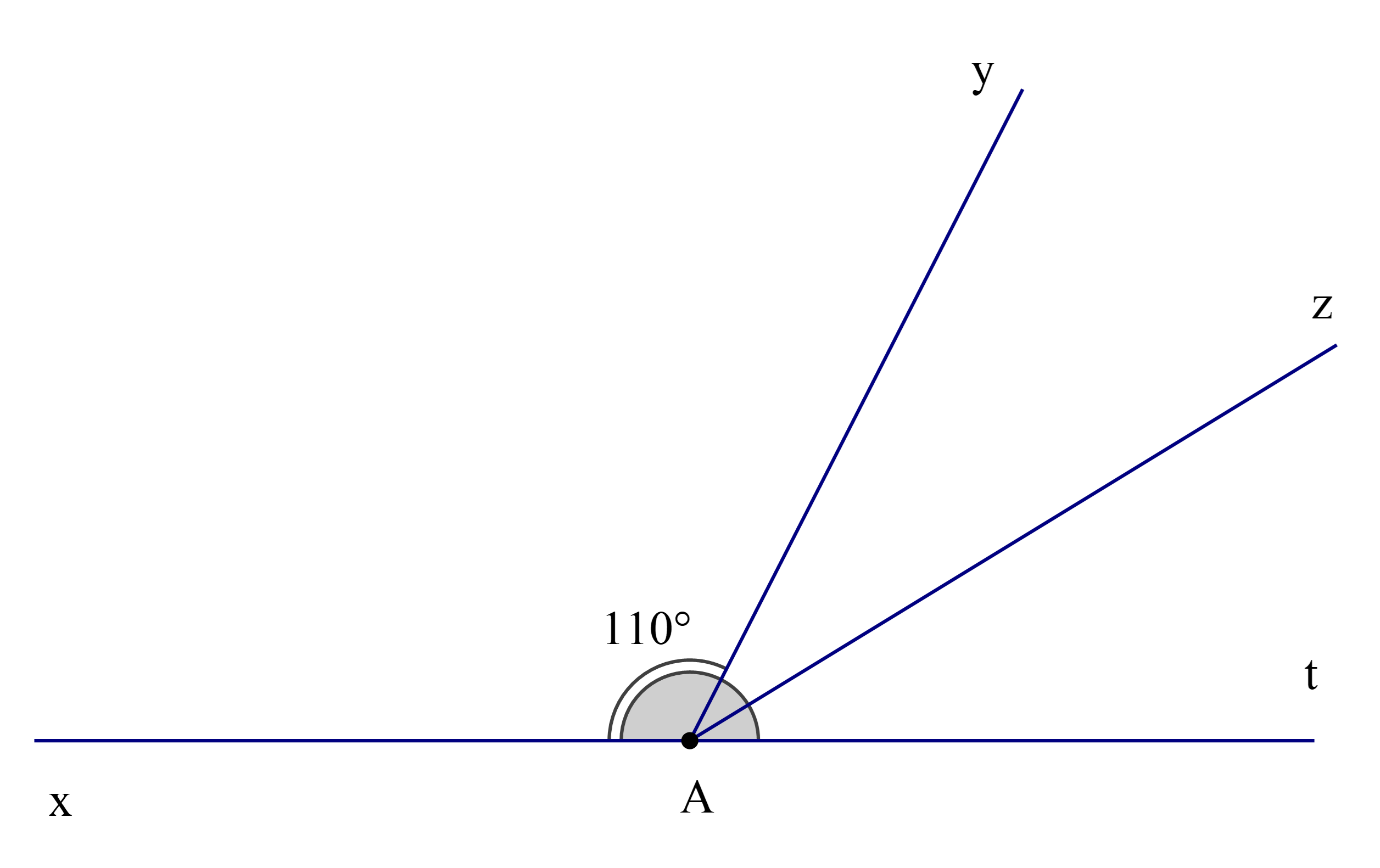
Theo bài ta có EF // BC (1)
Mà \(\widehat {{\rm{AEF}}}\) và \(\widehat {{\rm{EBC}}}\) là hai góc nằm ở vị trí đồng vị (2)
Từ (1) và (2) suy ra \(\widehat {{\rm{AEF}}} = \widehat {{\rm{EBC}}} = 50^\circ \) (tính chất hai đường thẳng song song).
Lại có \(\widehat {BEF} + \widehat {AEF} = 180^\circ \) (hai góc kề bù)
Suy ra \(\widehat {BEF} = 180^\circ - \widehat {AEF}\)
Hay \(\widehat {BEF} = 180^\circ - 50^\circ = 130^\circ .\)
Vậy ta chọn phương án D.
Lời giải
Hướng dẫn giải
Đáp án đúng là: B
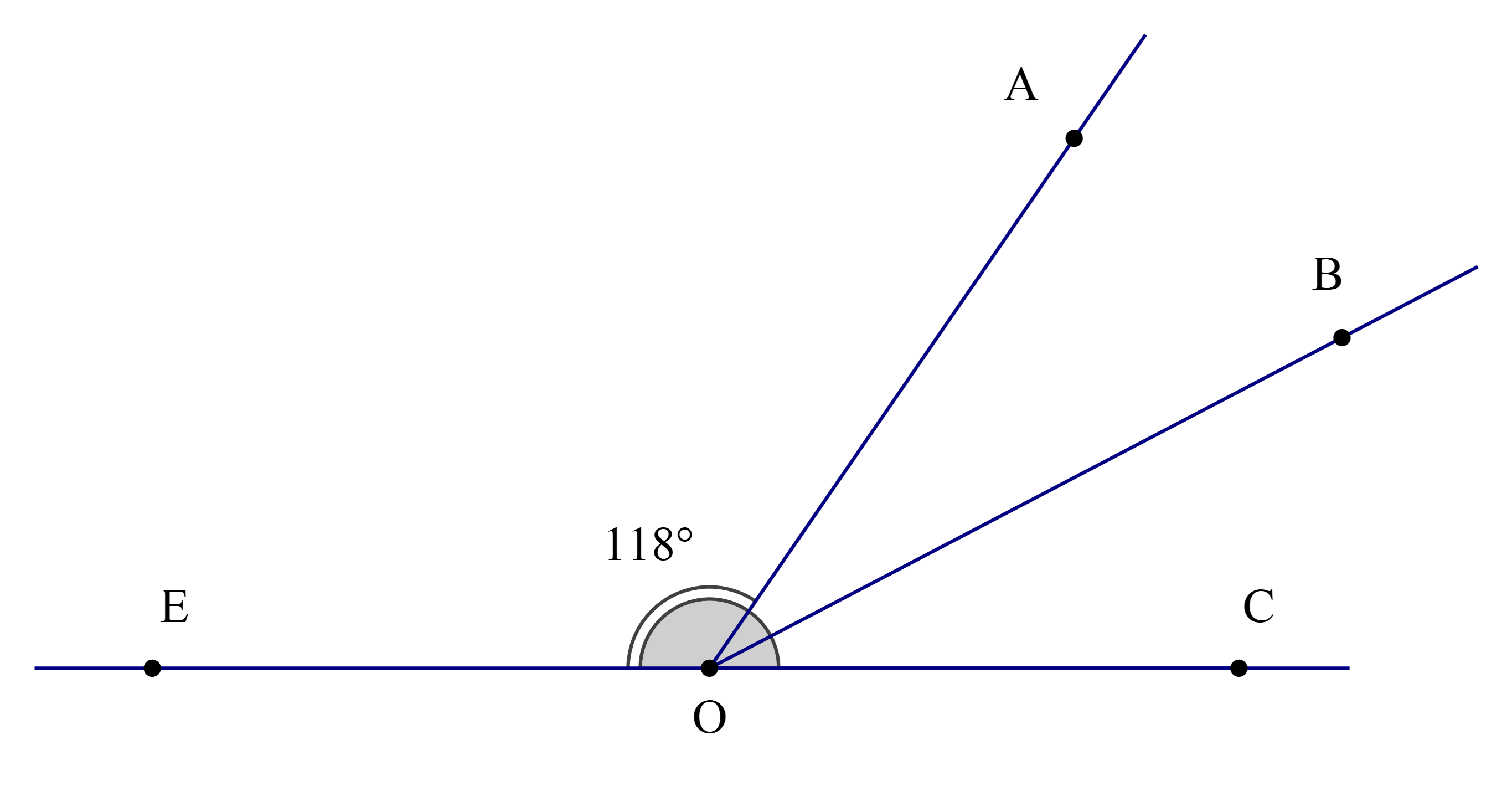
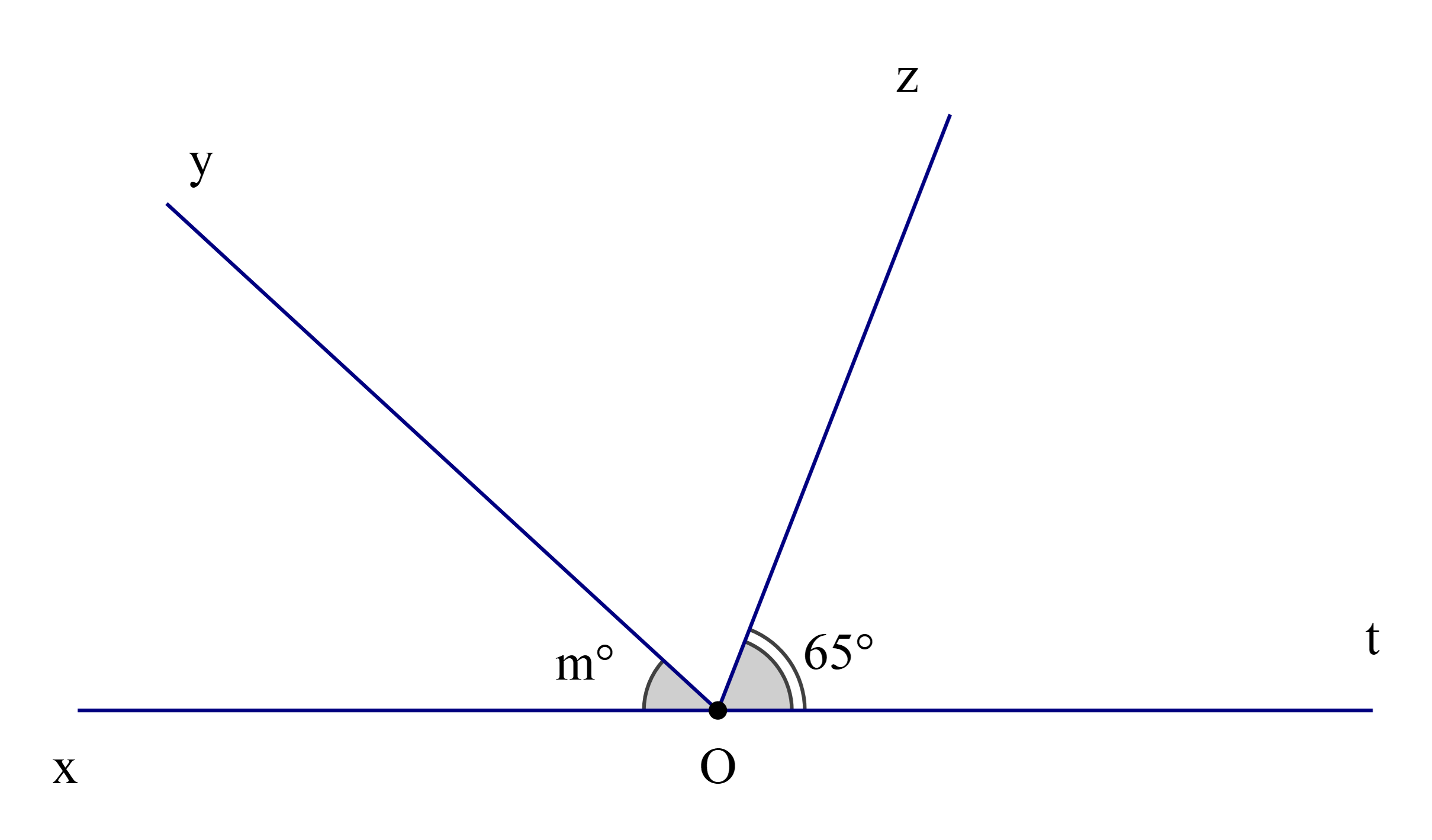
Ta có \(\widehat {{\rm{EOA}}}\) và \(\widehat {{\rm{AOC}}}\) là hai góc kề bù nên \(\widehat {{\rm{EOA}}} + \widehat {{\rm{AOC}}} = 180^\circ \)
Hay \(118^\circ + \widehat {{\rm{AOC}}} = 180^\circ \)
Suy ra \(\widehat {{\rm{AOC}}} = 180^\circ - 118^\circ = 62^\circ \)
Theo bài ta có OB là tia phân giác của \(\widehat {{\rm{AOC}}}\)
Do đó \(\widehat {{\rm{AOB}}} = \widehat {{\rm{BOC}}}\) (tính chất tia phân giác của một góc) (1)
Mà \(\widehat {{\rm{AOB}}} + \widehat {{\rm{BOC}}} = \widehat {{\rm{AOC}}}\) (hai góc kề nhau) (2)
Từ (1) và (2) suy ra \(\widehat {{\rm{AOB}}} = \widehat {{\rm{BOC}}} = \frac{1}{2}\widehat {{\rm{AOC}}}\)
Hay \(\widehat {{\rm{BOC}}} = \frac{1}{2}.62^\circ = 31^\circ \)
Vậy ta chọn phương án B.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 1
-
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 04
-
15 câu Trắc nghiệm Toán 7 Kết nối tri thức Bài 1: Tập hợp các số hữu tỉ có đáp án
-
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 2
-
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 01
-
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 02
-
15 câu Trắc nghiệm Toán 7 Cánh diều Bài 1: Tập hợp Q các số hữu tỉ có đáp án
-
Bộ 15 đề thi Học kì 2 Toán 7 có đáp án (Mới nhất) - đề 2