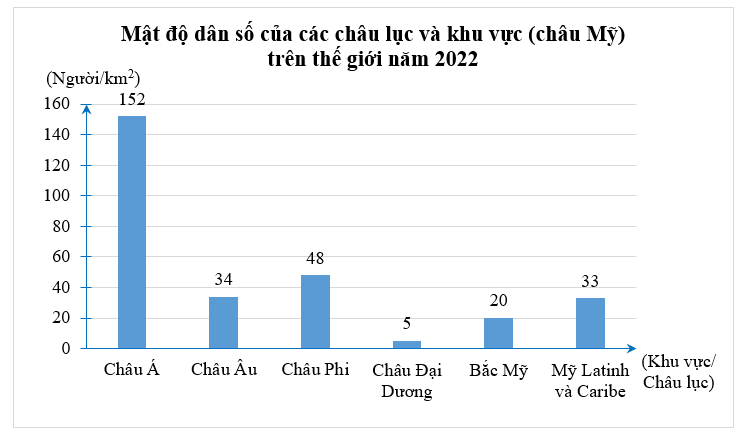
Dưới đây là biểu đồ cột biểu diễn mật độ dân số của các châu lục và khu vực (châu Mỹ) trên thế giới năm 2022 (cập nhật ngày 04/10/2022 theo số liệu từ Liên hợp Quốc).
Chọn khẳng định đúng?
Dưới đây là biểu đồ cột biểu diễn mật độ dân số của các châu lục và khu vực (châu Mỹ) trên thế giới năm 2022 (cập nhật ngày 04/10/2022 theo số liệu từ Liên hợp Quốc).
Chọn khẳng định đúng?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: C
Quan sát biểu đồ ta thấy:
• Châu Đại Dương có mật độ dân số thấp nhất: 5 người/km2. Do đó phương án A là sai.
• Châu Á có mật độ dân số cao nhất: 152 người/ km2. Do đó phương án B là sai.
• Khu vực Mỹ Latinh và Caribe có mật độ dân số cao hơn khu vực Bắc Mỹ: 33 > 20 (người/ km2). Do đó phương án C là đúng.
• Mật độ dân số của châu Á chênh lệch rất lớn với các châu lục và khu vực khác nên không thể tương đương nhau. Do đó phương án D là sai.
Vậy ta chọn phương án C.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đáp án đúng là: A
Ta có số đúng π = 3,141… nên sai số tuyệt đối của số gần đúng 3,14 là:
= |3,14 – π| < |3,141 – 3,14| = 0,001.
Vậy sai số tuyệt đối của số gần đúng 3,14 là 0,001.
Ta chọn phương án A.
Câu 2
C. a = 2,46;
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đáp án đúng là: C
Quy tròn số đến hàng phần trăm ta được số gần đúng là a = 2,46.
Câu 3
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. hàng chục nghìn;
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập