Một kệ sách có 3 quyển sách tham khảo Toán, 2 quyển sách tham khảo Văn và 4 quyển sách tham khảo Tiếng Anh. Bạn Hoa lấy ngẫu nhiên 2 quyển sách để học trong ngày hôm nay. Gọi A là biến cố: “Trong 2 quyển sách có 1 quyển sách Toán và 1 quyển sách Tiếng Anh”. Biến P(A) = . Biến cố là gì và có xác suất bằng bao nhiêu?
Một kệ sách có 3 quyển sách tham khảo Toán, 2 quyển sách tham khảo Văn và 4 quyển sách tham khảo Tiếng Anh. Bạn Hoa lấy ngẫu nhiên 2 quyển sách để học trong ngày hôm nay. Gọi A là biến cố: “Trong 2 quyển sách có 1 quyển sách Toán và 1 quyển sách Tiếng Anh”. Biến P(A) = . Biến cố là gì và có xác suất bằng bao nhiêu?
A. : “Trong 2 quyển sách được chọn không có sách Toán hoặc Tiếng Anh” và P() = ;
B. : “Trong 2 quyển sách được chọn không có sách Toán và Tiếng Anh” và P() = ;
C. : “Trong 2 quyển sách được chọn không có sách Toán” và P() = ;
D. : “Trong 2 quyển sách được chọn không có Tiếng Anh” và P() = .
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: A
là biến cố đối của biến cố A nên là: “Trong 2 quyển sách được chọn không có sách Toán hoặc Tiếng Anh”.
Khi đó P() = 1 – P(A) = 1 – = .
Vậy ta chọn đáp án A.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Trọng tâm Toán, Văn, Anh 10 cho cả 3 bộ KNTT, CTST, CD VietJack - Sách 2025 ( 13.600₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. P(A) là số lớn hơn 0;
B. P(A) = 1 – P();
C. P(A) = 0 ⇔ A = Ω;
D. P(A) là số nhỏ hơn 1.
Lời giải
Hướng dẫn giải
Đáp án đúng là: B
Đáp án A và D sai vì 0 ≤ P(A) ≤ 1.
Đáo án C sai vì P(A) = 0 ⇔ A = ∅.
A và là hai biến cố đối nên P(A) = 1 – P(). Do đó B đúng.
Lời giải
Hướng dẫn giải
Đáp án đúng là: B
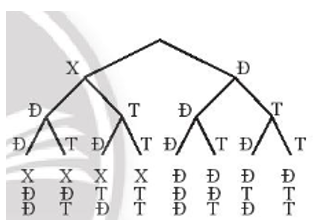
Dựa vào sơ đồ cây ta có các kết quả thuận lợi cho biến cố H là: {XĐT; XTĐ; ĐTT}.
Vậy có 3 kết quả thuận lợi cho biến cố H.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
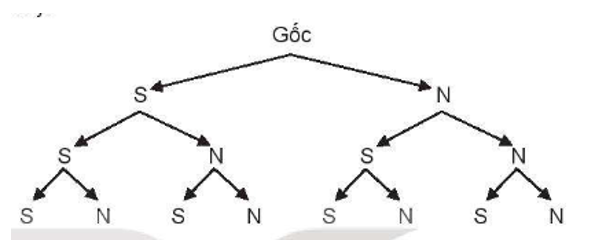
A. {S; N; S; N; S; N; S; N};
B. {SS; SN; NS; NN};
C. {SSS; SSN; SNS; SNN; NSS; NSN; NNS; NNN};
D. {S; N}.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo