✕

✨ Đăng kí VIP để truy cập không giới hạn. Đăng ký ngay

Câu hỏi:

03/11/2022 1,526

Vẽ 3 đường thẳng phân biệt cùng đi qua một điểm. Số cặp góc đối đỉnh (khác góc bẹt) là

A. 4;

B. 5;

C. 6;

D. 7.

Xem lời giải

Câu hỏi trong đề: 15 câu Trắc nghiệm Toán 7 Cánh diều Bài 1: Góc ở vị trí đặc biệt có đáp án (Phần 2) !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Hướng dẫn giải

Đáp án đúng là: C

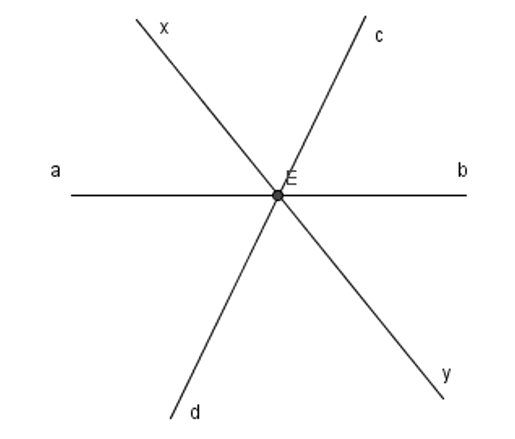
Vẽ 3 đường thẳng phân biệt cùng đi qua một điểm. Số cặp góc đối đỉnh (khác góc bẹt) là A. 4; B. 5; C. 6; D. 7. (ảnh 1)

Các cặp góc đối đỉnh (khác góc bẹt) là:

Góc cEb và góc dEa;

Góc bEy và góc aEx;

Góc yEd và góc xEc;

Góc cEy và góc dEx;

Góc bEd và góc aEc;

Góc yEa và góc xEb.

Vậy có 6 cặp góc đối đỉnh.

Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho hình vẽ:

Số đo của x là

A. 30°;

B. 120°;

C. 60°;

D. 90°.

Lời giải

Hướng dẫn giải

Đáp án đúng là: C

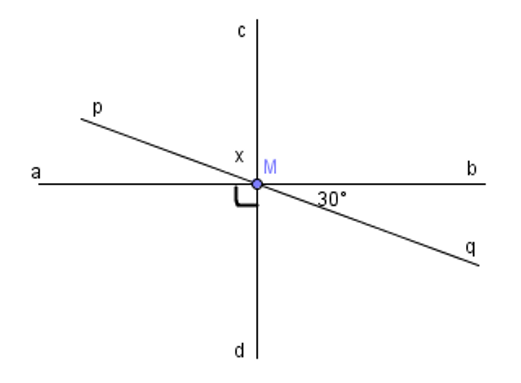
Ta có: $\hat{p M a} = \hat{q M b}$ (hai góc đối đỉnh)

Nên $\hat{p M a} = 30 °$

Góc cMa có số đo là 90° (góc vuông), mà hai góc pMa và góc pMc là hai góc kề nhau nên

\hat{p M a} + \hat{p M c} = \hat{c M a}

Thay số, $30 ° + x = 90 °$

Suy ra, $x = 90 ° - 30 ° = 60 °$ .

Câu 2

Cho hình vẽ. Nếu coi mỗi thanh chắn vòm cửa trong hình như một cạnh của góc thì số cặp góc kề bù là

A. 3

B. 4

C. 5

D. 6

Lời giải

Hướng dẫn giải

Đáp án đúng là: A

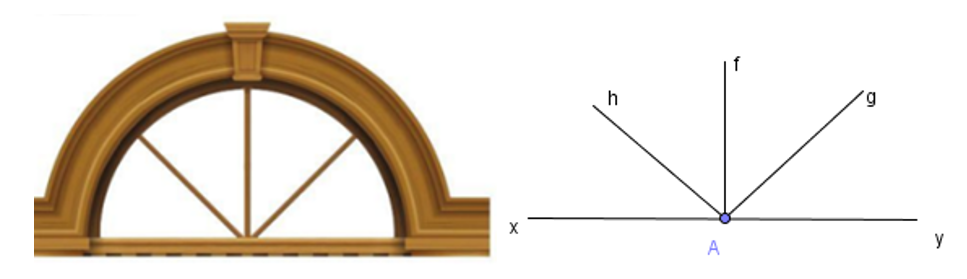
Các cặp góc kề bù là:

Góc xAh và góc hAy;

Góc xAf và góc fAy;

Góc xAg và góc gAy.

Vậy có 3 cặp góc kề bù.

Xem thêm các câu hỏi khác »