Em hãy cắt 6 hình tam giác đều có cạnh là 5 cm và ghép lại thành một hình lục giác đều (H.4.7). Hãy tính độ dài đường chéo chính của hình lục giác đều vừa ghép được.
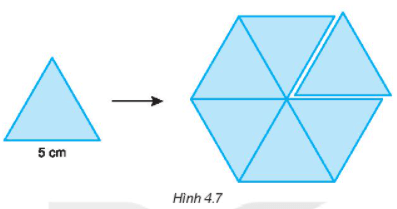
Em hãy cắt 6 hình tam giác đều có cạnh là 5 cm và ghép lại thành một hình lục giác đều (H.4.7). Hãy tính độ dài đường chéo chính của hình lục giác đều vừa ghép được.

Quảng cáo
Trả lời:
Ở hình 4.7, ta thấy độ dài đường chéo chính của hình lục giác đều bằng hai lần cạnh của tam giác đều
Do đó độ dài đường chéo chính của hình lục giác đều vừa ghép được là:
5. 2 = 10 (cm)
Vậy độ độ dài đường chéo chính của hình lục giác đều vừa ghép được là 10cm.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
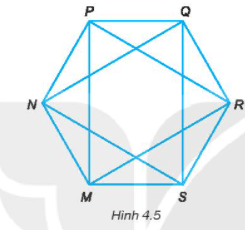
Trong hình 4. 5, ta có:
a) Các đường chéo phụ của hình lục giác đều MNPQRS là: NQ; QS; SN; MP; PR; MR.
b) Sử dụng thước thẳng đo hoặc compa ta thấy:
+) MP = PR = MR. Do đó tam giác MPR là tam giác đều.
+) NQ = QS = NS. Do đó tam giác NQS là tam giác đều.
Lời giải
a) Dùng compa đặt tâm ở điểm A và đầu chì ở điểm còn lại B, sau đó giữ nguyên khoảng cách compa, di chuyển compa đến đầu tâm đến điểm B, điểm còn lại nằm trên đoạn thẳng BC, ta thấy đầu chì không ở điểm C. Do đó AB và BC là hai đoạn thẳng không bằng nhau.
Vậy tam giác ABC không là tam giác đều.
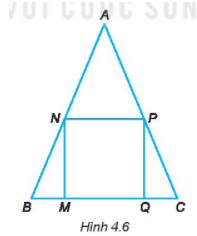
b)
+) Dùng compa để kiểm tra các đoạn thẳng MN, MQ, PQ, NP ta thấy
MN = MQ = PQ = NP. Do đó 4 cạnh của hình MNPQ bằng nhau.
+) Dùng ê ke để kiểm tra các góc của hình MNPQ ta thấy:
MN vuông góc với MQ và NP hay góc NMQ và góc MNP đều bằng 90o
PQ vuông góc với QM và NP hay góc MQP và góc NPQ đều bằng 90o
Suy ra: các góc NMQ, góc MNP, góc MQP, góc NPQ đều bằng 90o
Do đó hình MNPQ có 4 góc vuông ở các đỉnh
Vậy MNPQ là hình vuông.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.