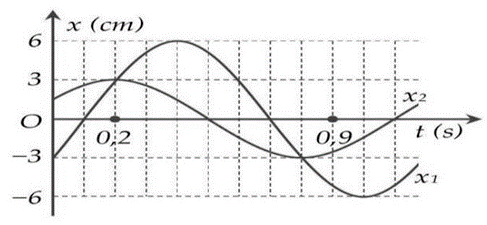
Dao động của một vật là tổng hợp của hai dao động điều hòa cùng phương có li độ lần lượt là \({x_1}\) và \({x_2}\). Hình bên là đồ thị biểu diễn sự phụ thuộc của \({x_1}\) và \({x_2}\) theo thời gian \(t\). Chọn gốc thế năng tại vị trí cân bằng. Vào thời điểm \(t = 0,55{\rm{\;s}}\), tỉ số giữa động năng và thế năng của vật có giá trị gần nhất với giá trị nào sau đây
A. 0,24
B. 0,80
C. 4,20
D. 1,29
Câu hỏi trong đề: (2023) Đề thi thử Vật Lí Sở Bình Dương có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Xét tại thời điểm \(t = 0,2s\) thì \(x = {x_1} + {x_2} = 6\angle - \frac{\pi }{3} + 3\angle 0 \approx 3\sqrt 7 \angle - 0,7137\)
Tại thời điểm \(t = 0,55{\rm{\;s}}\) thì \(x = 3\sqrt 7 {\rm{cos}}\left( {\frac{{5\pi }}{3}\left( {0,55 - 0,2} \right) - 0,7137} \right) \approx 3,466{\rm{\;cm}}\) \(\frac{{{W_d}}}{{{W_t}}} = \frac{{{A^2} - {x^2}}}{{{x^2}}} = \frac{{{{(3\sqrt 7 )}^2} - 3,{{466}^2}}}{{3,{{466}^2}}} \approx 4,24\). Chọn C
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. \(4\sqrt 2 {\rm{\;cm}}\)
B. \(2,0{\rm{\;cm}}\)
C. \(4,0{\rm{\;cm}}\)
D. \(8,0{\rm{\;cm}}\)
Lời giải
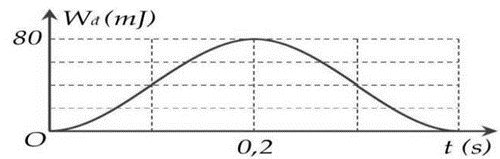
Từ \({W_d} = 0\) đến \({W_{d{\rm{max}}}}\) thì vật đi từ biên đến vtcb
\( \Rightarrow \frac{T}{4} = 0,2{\rm{\;s}} \Rightarrow T = 0,8{\rm{\;s}} \to \omega = \frac{{2\pi }}{T} = \frac{{5\pi }}{2}{\rm{rad}}/{\rm{s}}\) \({W_{d{\rm{max}}}} = \frac{1}{2}m{\omega ^2}{A^2} \Rightarrow 80 \cdot {10^{ - 3}} = \frac{1}{2} \cdot 0,4 \cdot {\left( {\frac{{5\pi }}{2}} \right)^2} \cdot {A^2} \Rightarrow A \approx 0,08m = 8{\rm{\;cm}}\). Chọn D
Câu 2
A. \(4,4{\rm{\;N}}/{\rm{m}}\)
B. \(14{\rm{\;N}}/{\rm{m}}\)
C. \(197{\rm{\;N}}/{\rm{m}}\)
D. \(19,4{\rm{\;N}}/{\rm{m}}\)
Lời giải
\(20T = 15s \Rightarrow T = 0,75s\)
\(T = 2\pi \sqrt {\frac{m}{k}} \Rightarrow 0,75 = 2\pi \sqrt {\frac{{0,2}}{k}} \Rightarrow k \approx 14N/m\). Chọn B
Câu 3
A. \(2k\pi \) với \(k = 0; \pm 1; \pm 2; \ldots \)
B. \(\left( {2k + 1} \right)\frac{\pi }{4}\) với \(k = 0; \pm 1; \pm 2; \ldots \)
C. \(\left( {2k + 1} \right)\pi \) với \(k = 0; \pm 1; \pm 2; \ldots \)
D. \(k\frac{\pi }{2}\) với \(k = 0; \pm 1; \pm 2; \ldots \)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \({s_0} = {\alpha _0}g\)
B. \({s_0} = {\alpha _0}\ell \)
C. \({s_0} = \frac{\ell }{{{\alpha _0}}}\)
D. \({s_0} = \frac{{{\alpha _0}}}{\ell }\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \(0,04{\rm{H}}\)
B. \(0,51{\rm{H}}\)
C. \(0,25{\rm{H}}\)
D. \(0,2{\rm{H}}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \(f\)
B. \({f_0}\)
C. \(f + {f_0}\)
D. \(\left| {f - {f_0}} \right|\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. điểm \(M\) cách \(A\) một đoạn \(0,5\lambda \) là điểm bụng
B. điểm \(Q\) cách \(A\) một đoạn 3,5 3 là điểm nút
C. điểm \(N\) cách \(A\) một đoạn \(2\lambda \) là điểm bụng
D. điểm \(P\) cách \(A\) một đoạn \(2,25\lambda \) là điểm nút
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập