Câu hỏi:
13/04/2023 1,517
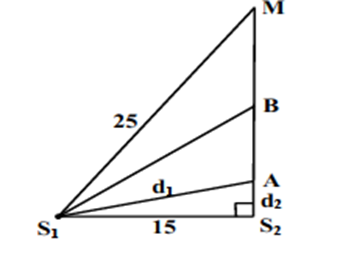
Trên mặt chất lỏng, có hai nguồn kết hợp S1 và S2 cách nhau 15 cm, dao động theo phương thẳng đứng với phương trình là \({u_{S1}} = {u_{S2}} = 2\cos \left( {10\pi t - \frac{\pi }{4}} \right)\) (cm). Tốc độ truyền sóng trên mặt chất lỏng là 20 cm/s. Coi biên độ sóng không đổi khi truyền đi. Trên đường thẳng vuông góc với \({S_1}{S_2}\) tại \({S_2}\) lấy điểm M sao cho \(M{S_1} = 25cm\) và \(M{S_2} = 20\) cm. Điểm A và B lần lượt nằm trong đoạn \({S_2}M\) với A gần \({S_2}\) nhất, B xa \({S_2}\) nhất, đều có tốc độ dao động cực đại bằng 40π cm/s. Khoảng cách AB là
Trên mặt chất lỏng, có hai nguồn kết hợp S1 và S2 cách nhau 15 cm, dao động theo phương thẳng đứng với phương trình là \({u_{S1}} = {u_{S2}} = 2\cos \left( {10\pi t - \frac{\pi }{4}} \right)\) (cm). Tốc độ truyền sóng trên mặt chất lỏng là 20 cm/s. Coi biên độ sóng không đổi khi truyền đi. Trên đường thẳng vuông góc với \({S_1}{S_2}\) tại \({S_2}\) lấy điểm M sao cho \(M{S_1} = 25cm\) và \(M{S_2} = 20\) cm. Điểm A và B lần lượt nằm trong đoạn \({S_2}M\) với A gần \({S_2}\) nhất, B xa \({S_2}\) nhất, đều có tốc độ dao động cực đại bằng 40π cm/s. Khoảng cách AB là
Câu hỏi trong đề: (2023) Đề thi thử Vật Lí Sở Nam Định có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Chọn A. \[\lambda = \frac{v}{f} = \frac{{20}}{5} = 4\]cm. Hai nguồn cùng pha.
Điểm A và B có tốc độ dao động \[\user2{v = 40\pi cm/s = \omega }\user2{.2A = }{\user2{v}_{max}}\]nên điểm A và B là các điểm dao động với biên độ cực đại, nên ta có:
Trên đoạn \({S_2}M\)ta có: \[\frac{{\user2{M}{\user2{S}_\user2{1}}\user2{ - M}{\user2{S}_\user2{1}}}}{\user2{\lambda }}\user2{ < k < }\frac{{{\user2{S}_\user2{1}}{\user2{S}_\user2{2}}}}{\user2{\lambda }}\user2{ = > }\]\[\frac{{\user2{25 - 20}}}{4}\user2{ < k < }\frac{{\user2{15}}}{4}\user2{ = > }\]\[\user2{1,25 < k < 3,75}\]
=>Chọn k=2;3.
Trên hình vẽ \[M{{\rm{S}}_2} \bot {{\rm{S}}_1}{{\rm{S}}_2}\], ta có: \[d_1^2 - d_2^2 = S_1^{}S_2^2\]
=> \[\left\{ \begin{array}{l}\user2{d}_\user2{1}^{}\user2{ - d}_\user2{2}^{}\user2{ = k\lambda }\\\user2{d}_\user2{1}^{}\user2{ + d}_\user2{2}^{}\user2{ = }\frac{{{\user2{S}_\user2{1}}\user2{S}_\user2{2}^\user2{2}}}{{\user2{k\lambda }}}\end{array} \right.\user2{ = > d}_\user2{2}^{}\user2{ = }\frac{{{\user2{S}_\user2{1}}\user2{S}_\user2{2}^\user2{2}}}{{\user2{2k\lambda }}}\user2{ - }\frac{{\user2{k\lambda }}}{\user2{2}} = \frac{{\user2{15}_{}^\user2{2}}}{{\user2{8k}}}\user2{ - 2k}\].
=>\[\left\{ \begin{array}{l}\user2{k = 2 = > d}_\user2{2}^{} = \frac{{\user2{15}_{}^\user2{2}}}{{\user2{8}\user2{.2}}}\user2{ - 2}\user2{.2 = 10,0625}\;\user2{cm}\\\user2{k = 3 = > d}_\user2{2}^{} = \frac{{\user2{15}_{}^\user2{2}}}{{\user2{8}\user2{.3}}}\user2{ - 3}\user2{.2 = 3,375}\;\user2{cm}\end{array} \right.\]
ð AB=10,0625 -3,375 =6,6875 cm.
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 20 đề thi tốt nghiệp môn Vật lí (có đáp án chi tiết) ( 38.000₫ )
- 1000 câu hỏi lí thuyết môn Vật lí (Form 2025) ( 45.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Chọn B.
\[{\user2{S}_\user2{0}}\user2{ = l}{\user2{\alpha }_\user2{0}}\user2{ = 1}\user2{.}\frac{{\user2{6\pi }}}{{\user2{180}}}\user2{ = }\frac{\user2{\pi }}{{\user2{30}}}\]m và kéo vật theo chiều dương, chọn mốc thời gian là lúc thả vật =>φ =0..
=>\(s\, = \frac{\pi }{{30}}c{\rm{os}}(\pi t)\,(m)\)
Lời giải
Chọn D. Khi mạch xảy ra cộng hưởng thì: uL + uC = 0 => u= uL + uC + uR = uR
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Đề thi thử tốt nghiệp THPT môn Vật lí Sở Giáo dục và Đào tạo Nam Định có đáp án
-
(2025 mới) Đề ôn thi tốt nghiệp THPT Vật lí (Đề số 1)
-
Đề minh họa tốt nghiệp THPT môn Vật lý có đáp án năm 2025 (Đề 3)
-
Đề minh họa tốt nghiệp THPT môn Vật lý có đáp án năm 2025 (Đề 4)
-
Đề minh họa tốt nghiệp THPT môn Vật lý có đáp án năm 2025 (Đề 2)
-
Đề thi thử tốt nghiệp THPT môn Vật lí THPT Yên Lạc - Vĩnh Phúc - Lần 1 có đáp án
-
(2025 mới) Đề ôn thi tốt nghiệp THPT Vật lí (Đề số 6)
-
Đề thi thử tốt nghiệp THPT môn Vật lí THPT Trưng Yên - Hưng Yên có đáp án