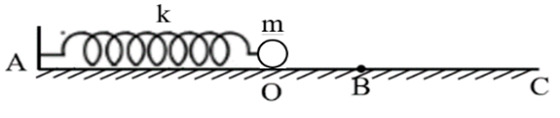
Một con lắc lò xo gồm lò xo nhẹ có độ cứng k = 40 N/m, vật nhỏ có khối lượng m = 100 g đặt trên mặt bàn ngang như hình vẽ bên. Chiều dài tự nhiên của lò xo là OA = 30 cm. Mặt bàn có hai phần, phần nhẵn AB = 34 cm, phần nhám BC (đủ dài) có hệ số ma sát \[{\rm{\mu = 0}}{\rm{,4}}{\rm{.}}\] Lấy g = 10 m/s2. Ban đầu, giữ vật m sao cho lò xo bị nén 8 cm rồi thả nhẹ. Kể từ lúc thả, khoảng thời gian ngắn nhất để lò xo dãn cực đại gần nhất với giá trị nào sau đây?
A. 0,16 s.
B. 0,15 s.
C. 0,17 s.
D. 0,14 s.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn
GĐ1: Dao động không ma sát đến B
\(\omega = \sqrt {\frac{k}{m}} = \sqrt {\frac{{40}}{{0,1}}} = 20\) (rad/s)
\(x = OB = AB - OA = 34 - 30 = 4cm\)
\(v = \omega \sqrt {{A^2} - {x^2}} = 20\sqrt {{8^2} - {4^2}} = 80\sqrt 3 cm/s\)
GĐ2: Dao động có ma sát với vtcb O’
\({F_{ms}} = \mu mg = 0,4.0,1.10 = 0,4\) (N)
\(O'O = \frac{{{F_{ms}}}}{k} = \frac{{0,4}}{{40}} = 0,01m = 1cm \to x' = 1 + 4 = 5cm\)
\(A' = \sqrt {x{'^2} + {{\left( {\frac{v}{\omega }} \right)}^2}} = \sqrt {{5^2} + {{\left( {\frac{{80\sqrt 3 }}{{20}}} \right)}^2}} = \sqrt {73} cm\)
\(t = \frac{{\arccos \frac{x}{{ - A}} + \arccos \frac{{x'}}{{A'}}}}{\omega } = \frac{{\arccos \frac{4}{{ - 8}} + \arccos \frac{5}{{\sqrt {73} }}}}{{20}} \approx 0,152s\). Chọn B
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 1000 câu hỏi lí thuyết môn Vật lí (Form 2025) ( 45.000₫ )
- Sổ tay Vật lí 12 (chương trình mới) ( 18.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn
\(\frac{\lambda }{2} = 12 \Rightarrow \lambda = 24cm\)
\(A = 1,5cm = \frac{{{A_b}}}{2}\) và đối xứng nhau qua nút nên cách nhau \(\frac{\lambda }{6} = \frac{{24}}{6} = 4cm\). Chọn C
Câu 2
A. \[{\rm{i = 2}}\sqrt {\rm{2}} {\rm{cos}}\left( {{\rm{100\pi t + }}\frac{{\rm{\pi }}}{{\rm{3}}}} \right)\,{\rm{A}}{\rm{.}}\]
B. \[{\rm{i = 2}}\sqrt {\rm{2}} {\rm{cos}}\left( {{\rm{100\pi t + }}\frac{{\rm{\pi }}}{{\rm{2}}}} \right)\,{\rm{A}}{\rm{.}}\]
C. \[{\rm{i = 2}}\sqrt {\rm{2}} {\rm{cos}}\left( {{\rm{100\pi t - }}\frac{{\rm{\pi }}}{{\rm{6}}}} \right)\,{\rm{A}}{\rm{.}}\]
D. \[{\rm{i = 2}}\sqrt {\rm{2}} {\rm{cos}}\left( {{\rm{100\pi t + }}\frac{{\rm{\pi }}}{{\rm{6}}}} \right)\,{\rm{A}}{\rm{.}}\]
Lời giải
Hướng dẫn
\(\left\{ \begin{array}{l}{U^2} = U_r^2 + {\left( {{U_L} - {U_C}} \right)^2}\\U_{rL}^2 = U_r^2 + U_L^2\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{60^2} = U_r^2 + {\left( {{U_L} - 120} \right)^2}\\{\left( {60\sqrt 3 } \right)^2} = U_r^2 + U_L^2\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{U_r} = 30\sqrt 3 V\\{U_L} = 90V\end{array} \right.\)
\(\tan \varphi = \frac{{{U_L} - {U_C}}}{{{U_r}}} = \frac{{90 - 120}}{{30\sqrt 3 }} = - \frac{{\sqrt 3 }}{3} \Rightarrow \varphi = - \frac{\pi }{6} = {\varphi _u} - {\varphi _i} \Rightarrow {\varphi _i} = \frac{\pi }{6}\). Chọn D
\({Z_C} = \frac{1}{{\omega C}} = \frac{1}{{100\pi .\frac{{{{10}^{ - 3}}}}{{6\pi }}}} = 60\Omega \)
\(I = \frac{{{U_C}}}{{{Z_C}}} = \frac{{120}}{{60}} = 2A \Rightarrow {I_0} = 2\sqrt 2 A\)
Câu 3
A. 15,8 cm.
B. 15,2 cm.
C. 15,5 cm.
D. 16,2 cm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \[80\,\Omega \,.\,\]
B. \[30\sqrt 2 \,\Omega \,.\,\]
C. \[60\,\Omega \,.\,\]
D. \[2\sqrt {15} \,\Omega \,.\,\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \[\left( {{\rm{2k + 0}}{\rm{,5}}} \right){\rm{.\pi }}\] với \[{\rm{k}} = 0;\, \pm 1;\, \pm 2;\,...\]
B. \[2{\rm{k\pi }}\] với \[{\rm{k}} = 0;\, \pm 1;\, \pm 2;\,...\]
C. \[\left( {{\rm{2k + 1}}} \right){\rm{.\pi }}\] với \[{\rm{k}} = 0;\, \pm 1;\, \pm 2;\,...\]
D. \[\left( {{\rm{k + 0}}{\rm{,5}}} \right){\rm{.\pi }}\] với \[{\rm{k}} = 0;\, \pm 1;\, \pm 2;\,...\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập