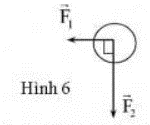
Một vật chịu tác dụng của hai lực F1 và F2 như hình 6. Cho F1 = 5 N, F2 = 12 N. Tìm F3 để vật cân bằng, biết khối lượng của vật không đáng kể.

Lời giải: Từ hình vẽ ta thấy [{ overrightarrow F _1} bot { overrightarrow F _2} ] nên độ lớn tổng hợp lực của chúng là: [F = sqrt {F_1^2 + F_2^2} = 13 ,N ] Lực tổng hợp có phương hợp với phương thẳng đứng (phương của lực F2) một góc: [ tan alpha = frac{{{F_1}}}{{{F_2}}} = frac{5}{{12}} Rightarrow alpha = {22,6^0} ] Nên để vật cân bằng thì lực F3 phải có độ lớn bằng 13 N và có phương hợp với phương thẳng đứng góc 22,60 và có chiều ngược lại với lực F, điểm đặt trùng với điểm đặt của các lực F1, F2 và F.

Câu hỏi:

13/07/2024 6,225

Một vật chịu tác dụng của hai lực F₁ và F₂ như hình 6. Cho F₁ = 5 N, F₂ = 12 N. Tìm F₃ để vật cân bằng, biết khối lượng của vật không đáng kể.

Xem lời giải

Câu hỏi trong đề: 2020 câu Trắc nghiệm tổng hợp Vật lí 2023 có đáp án !!

Giao bài

Quảng cáo

Trả lời:

Giải bởi Vietjack

Lời giải:

Từ hình vẽ ta thấy \[{\overrightarrow F _1} \bot {\overrightarrow F _2}\] nên độ lớn tổng hợp lực của chúng là: \[F = \sqrt {F_1^2 + F_2^2} = 13\,N\]

Lực tổng hợp có phương hợp với phương thẳng đứng (phương của lực F₂) một góc:

\[\tan \alpha = \frac{{{F_1}}}{{{F_2}}} = \frac{5}{{12}} \Rightarrow \alpha = {22,6^0}\]

Nên để vật cân bằng thì lực F₃ phải có độ lớn bằng 13 N và có phương hợp với phương thẳng đứng góc 22,6⁰ và có chiều ngược lại với lực F, điểm đặt trùng với điểm đặt của các lực F₁, F₂ và F.

Đang tải chế độ Học...

Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

ĐẶC QUYỀN VIP

Đăng ký VIP để học và luyện thi không giới hạn

Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.

Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
Đăng ký ngay

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Một vật dao động điều hòa, cứ sau một khoảng thời gian 0,5 s thì động năng lại bằng thế năng của vật. Khoảng thời gian nhỏ nhất giữa hai lần động năng bằng ba lần thế năng của vật là?

Xem đáp án

Lời giải

Lời giải:

\(\frac{T}{4} = 0,5 \Rightarrow T = 2\)

\({{\rm{W}}_{\rm{d}}} = 3{W_t} \Rightarrow {{\rm{W}}_t} = \frac{{\rm{W}}}{4} \Rightarrow \frac{1}{2}k{x^2} = \frac{1}{4}.\frac{1}{2}k{A^2} \Rightarrow \left| x \right| = \frac{A}{2}\)

Khoảng thời gian nhỏ nhất giữa hai lần động năng bằng ba lần thế năng được tính từ vị trí \[\frac{A}{2}\] đến \[ - \frac{A}{2}\] (đối xứng với nhau qua VTCB) \( \Rightarrow \frac{T}{6} = \frac{1}{3}s\)\(\)

Câu 2

Một xe chuyển động chậm dần đều cho đến khi dừng lại. Quãng đường xe đi được trong giây đầu tiên gấp 19 lần quãng đường xe đi được trong giây cuối cùng. Quãng đường đi được trong cả giai đoạn này là 100 m. Tìm quãng đường ô tô đi được cho đến lúc dừng hẳn.

Xem đáp án

Lời giải

Lời giải:

Ta có: \[S = {v_o}t + \frac{1}{2}a{t^2}\]

Khi vật dừng lại: \[v = {v_0} + at = 0 \Rightarrow {v_0} = - at\] (1)

Quãng đường đi trong một giây đầu tiên: \[{S_1} = {v_0} + \frac{1}{2}a = 95\left( m \right)\] (2)

Quãng đường vật đi trong giây cuối là:

\[{S_2} = S - {S_{t - 1}} = {v_0}t + \frac{1}{2}a{t^2} - {v_0}\left( {t - 1} \right) - \frac{1}{2}a{\left( {t - 1} \right)^2} = {v_0} + at - \frac{1}{2}a = 5\left( m \right)\] (3)

Từ (1), (2), (3): \[\left\{ \begin{array}{l} - at + \frac{1}{2}a = 95\\ - \frac{1}{2}a = 5\end{array} \right. \Rightarrow \left\{ \begin{array}{l}t = 10\,s\\a = - 10\,m/{s^2}\end{array} \right. \Rightarrow {v_0} = 100\,m/s\]

Quãng đường ô tô đi được cho đến khi dừng hẳn: \[S = 100.10 - \frac{1}{2}{.10.10^2} = 500\,m\]

Câu 3