Một lò xo nhẹ có đầu dưới gắn vào giá cố định, đầu trên gắn với vật nhỏ \(M\), trên nó đặt vật nhỏ \(m\) (như hình h.c). Bỏ qua mọi lực cản, lấy \(g = 10{\rm{\;}}m/{s^2}\). Kích thích cho hệ dao động điều hòa theo phương thẳng đứng. Hình vẽ (h.d) là đồ thị biểu diễn sự phụ thuộc của phản lực mà \(M\) tác dụng lên \(m\) theo thời gian với \({t_2} - {t_1} = \frac{{3\pi }}{{20}}{\rm{\;}}s\). Tại thời điểm mà độ lớn của áp lực \(m\) đè lên \(M\) bằng 0,6 lần trọng lực của \(m\) thì tốc độ của \(M\) là
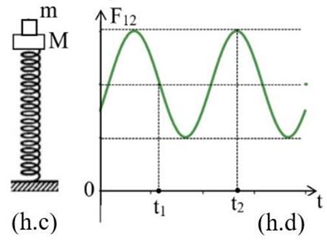
Một lò xo nhẹ có đầu dưới gắn vào giá cố định, đầu trên gắn với vật nhỏ \(M\), trên nó đặt vật nhỏ \(m\) (như hình h.c). Bỏ qua mọi lực cản, lấy \(g = 10{\rm{\;}}m/{s^2}\). Kích thích cho hệ dao động điều hòa theo phương thẳng đứng. Hình vẽ (h.d) là đồ thị biểu diễn sự phụ thuộc của phản lực mà \(M\) tác dụng lên \(m\) theo thời gian với \({t_2} - {t_1} = \frac{{3\pi }}{{20}}{\rm{\;}}s\). Tại thời điểm mà độ lớn của áp lực \(m\) đè lên \(M\) bằng 0,6 lần trọng lực của \(m\) thì tốc độ của \(M\) là
A. \(40{\rm{\;cm}}/{\rm{s}}\).
B. \(20{\rm{\;cm}}/{\rm{s}}\).
C. \(25{\rm{\;cm}}/{\rm{s}}\).
D. \(30{\rm{\;cm}}/{\rm{s}}\).
Quảng cáo
Trả lời:
Giải bởi Vietjack
\(\Delta t = \frac{{3T}}{4} = \frac{{3\pi }}{{20}}s \Rightarrow T = \frac{\pi }{5}s \to \omega = \frac{{2\pi }}{T} = 10rad/s\)
\(N - mg = - m{\omega ^2}x \Rightarrow N = m\left( {g - {\omega ^2}x} \right) \Rightarrow \frac{{{N_{\max }}}}{{{N_{\min }}}} = \frac{{g + {\omega ^2}A}}{{g - {\omega ^2}A}} \Rightarrow 3 = \frac{{10 + {{10}^2}A}}{{10 - {{10}^2}A}} \Rightarrow A = 0,05m = 5cm\)
Tại \(N = m\left( {g - {\omega ^2}x} \right) = 0,6mg \Rightarrow 10 - {10^2}x = 0,6.10 \Rightarrow x = 0,04m = 4cm\)
\(v = \omega \sqrt {{A^2} - {x^2}} = 10\sqrt {{5^2} - {4^2}} = 30cm/s\). Chọn D
Hot: 1000+ Đề thi giữa kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. \(4,8{\rm{\;m}}/{\rm{s}}\).
B. \(7,2{\rm{\;m}}/{\rm{s}}\).
C. \(3,6{\rm{\;m}}/{\rm{s}}\).
D. \(6,4{\rm{\;m}}/{\rm{s}}\).
Lời giải
\(\omega = 2\pi f = 2\pi .10 = 20\pi \) (rad/s)
\(A = \frac{{{v_{\max }}}}{\omega } = \frac{{30\pi }}{{20\pi }} = 1,5cm = \frac{{{A_b}}}{2} \to \frac{\lambda }{6} = 6 \Rightarrow \lambda = 36cm\)
\(v = \lambda f = 36.10 = 360cm/s = 3,6m/s\). Chọn C
Câu 2
A. ngược pha nhau.
B. lệch pha nhau.
C. vuông pha nhau.
D. cùng pha nhau.
Lời giải
Chọn D
Câu 3
A. tia Rơn - ghen.
B. tia hồng ngoại.
C. ánh sáng tím.
D. tia tử ngoại.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \(\frac{{15}}{8}\).
B. \(\frac{2}{3}\).
C. \(\frac{3}{2}\).
D. \(\frac{8}{{15}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. lực hấp dẫn.
B. lực hóa học.
C. lực Loren - xơ.
D. lực điện trường.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \(10{\rm{\;}}cm\).
B. \(4{\rm{\;}}cm\).
C. \(2,5{\rm{\;}}cm\).
D. \(5{\rm{\;}}cm\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \(1,54{\rm{\;s}}\).
B. \(1,66{\rm{\;s}}\).
C. 1,72 s.
D. \(1,44{\rm{\;s}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo