Câu hỏi:
28/06/2023 335
Một con lắc lò xo đặt thẳng đứng gồm lò xo nhẹ có độ cứng \(k = 100\,N/m\) và vật nhỏ \({m_1}\) khối lượng \(200\,g\). Một đầu lò xo gắn chặt vào sàn. Ban đầu, giữ \({m_1}\) ở vị trí lò xo nén \(12\,cm\) (trong giới hạn đàn hồi của lò xo) rồi đặt thêm vật nhỏ \({m_2}\) có khối lượng cũng bằng \(200\,g\) lên trên \({m_1}\) như hình bên. Thả nhẹ để các vật bắt đầu chuyển động theo phương thẳng đứng. Vào thời điểm \({t_1}\), vật \({m_2}\) rời khỏi \({m_1}\) chuyển động thẳng đứng lên trên, sau khi rời m1, m2 chuyển động ném lên đạt độ cao cực đại vào thời điểm \({t_2}\). Khoảng cách giữa 2 vật tại thời điểm \({t_2}\) có giá trị gần nhất với giá trị nào sau đây?
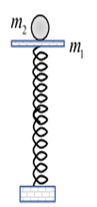
Một con lắc lò xo đặt thẳng đứng gồm lò xo nhẹ có độ cứng \(k = 100\,N/m\) và vật nhỏ \({m_1}\) khối lượng \(200\,g\). Một đầu lò xo gắn chặt vào sàn. Ban đầu, giữ \({m_1}\) ở vị trí lò xo nén \(12\,cm\) (trong giới hạn đàn hồi của lò xo) rồi đặt thêm vật nhỏ \({m_2}\) có khối lượng cũng bằng \(200\,g\) lên trên \({m_1}\) như hình bên. Thả nhẹ để các vật bắt đầu chuyển động theo phương thẳng đứng. Vào thời điểm \({t_1}\), vật \({m_2}\) rời khỏi \({m_1}\) chuyển động thẳng đứng lên trên, sau khi rời m1, m2 chuyển động ném lên đạt độ cao cực đại vào thời điểm \({t_2}\). Khoảng cách giữa 2 vật tại thời điểm \({t_2}\) có giá trị gần nhất với giá trị nào sau đây?
Quảng cáo
Trả lời:
Giải bởi Vietjack
GĐ1: Hai vật cùng dao động từ M lên đến vị trí tự nhiên
Tại vtcb O nén \(\Delta {l_0} = \frac{{\left( {{m_1} + {m_2}} \right)g}}{k} = \frac{{\left( {0,2 + 0,2} \right).10}}{{100}} = 0,04m = 4cm\)
\(A = 12 - 4 = 8cm\)
\(\omega = \sqrt {\frac{k}{{{m_1} + {m_2}}}} = \sqrt {\frac{{100}}{{0,2 + 0,2}}} = 5\sqrt {10} \) (rad/s)
\(v = \omega \sqrt {{A^2} - \Delta l_0^2} = 5\sqrt {10} .\sqrt {{8^2} - {4^2}} = 20\sqrt {30} \) (cm/s)
GĐ2: Tại vttn thì lực đàn hồi hướng xuống nên vật m2 tách khỏi m1
*Vật m2 bị ném lên thẳng đứng đến khi dừng lại lần đầu thì \(t = \frac{v}{g} = 0,02\sqrt {30} s\)
*Vật m1 dao động điều hòa quanh vị trí cân bằng mới O1 nén
\(\Delta {l_1} = \frac{{{m_1}g}}{k} = \frac{{0,2.10}}{{100}} = 0,02m = 2cm\) và \({\omega _1} = \sqrt {\frac{k}{{{m_1}}}} = \sqrt {\frac{{100}}{{0,2}}} = 10\sqrt 5 \) (rad/s)
\({A_1} = \sqrt {\Delta l_1^2 + {{\left( {\frac{v}{{{\omega _1}}}} \right)}^2}} = \sqrt {{2^2} + {{\left( {\frac{{20\sqrt {30} }}{{10\sqrt 5 }}} \right)}^2}} = 2\sqrt 7 cm\)
Chọn gốc tọa độ tại vị trí cân bằng mới O1, chiều dương hướng lên
\[\left\{ \begin{array}{l}{x_1} = {A_1}\cos \left( {{\omega _1}t - \arccos \frac{{\Delta {l_1}}}{{{A_1}}}} \right) = 2\sqrt 7 \cos \left( {10\sqrt 5 .0,02\sqrt {30} - \arccos \frac{2}{{2\sqrt 7 }}} \right) \approx 1,5865cm\\{x_2} = \Delta {l_1} + vt - \frac{1}{2}g{t^2} = 2 + 20\sqrt {30} .0,02\sqrt {30} - \frac{1}{2}.1000.{\left( {0,02\sqrt {30} } \right)^2} = 8cm\end{array} \right.\]
\({x_2} - {x_1} = 8 - 1,5865 = 6,4135cm\). Chọn B
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 20 đề thi tốt nghiệp môn Vật lí (có đáp án chi tiết) ( 38.000₫ )
- 500 Bài tập tổng ôn Vật lí (Form 2025) ( 38.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
\(\Delta m = 13{m_p} + 14{m_n} - {m_{Al}} = 13.1,0073 + 14.1,0087 - 26,9972 = 0,2195u\)
\({W_{lk}} = \Delta m{c^2} = 0,2195.931,5 \approx 204,5MeV\). Chọn A
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Đề thi thử tốt nghiệp THPT môn Vật lí Sở Giáo dục và Đào tạo Nam Định có đáp án
-
(2025 mới) Đề ôn thi tốt nghiệp THPT Vật lí (Đề số 1)
-
Đề minh họa tốt nghiệp THPT môn Vật lý có đáp án năm 2025 (Đề 3)
-
Đề minh họa tốt nghiệp THPT môn Vật lý có đáp án năm 2025 (Đề 4)
-
Đề minh họa tốt nghiệp THPT môn Vật lý có đáp án năm 2025 (Đề 2)
-
(2025 mới) Đề ôn thi tốt nghiệp THPT Vật lí (Đề số 6)
-
Đề thi thử tốt nghiệp THPT môn Vật lí THPT Yên Lạc - Vĩnh Phúc - Lần 1 có đáp án
-
Đề thi thử tốt nghiệp THPT môn Vật lí THPT Trưng Yên - Hưng Yên có đáp án
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận