Câu hỏi:

13/07/2024 675

Một máy bay đang bay ngang với vận tốc V₁ ở độ cao h so với mặt đất muốn thả bom trúng một đoàn xe tăng đang chuyển động với vận tốc V₂ trong cùng mặt phẳng thẳng đứng với máy bay. Hỏi còn cách xe tăng bao xa thì cắt bom (đó là khoảng cách từ đường thẳng đứng qua máy bay đến xe tăng) khi máy bay và xe tăng chuyển động cùng chiều.

Xem lời giải

Câu hỏi trong đề: 2020 câu Trắc nghiệm tổng hợp Vật lí 2023 có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Lời giải

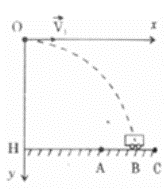
Media VietJack

Chọn gốc tọa độ O là điểm cắt bom, t = 0 là lúc cắt bom

Phương trình chuyển động là: \(\left\{ \begin{array}{l}x = {V_1}t\left( 1 \right)\\y = \frac{1}{2}g{t^2}\left( 2 \right)\end{array} \right.\)

Phương trình quỹ đạo: \(y = \frac{1}{2}\frac{g}{{v_0^2}}{x^2}\)

Bom sẽ rơi nhanh theo nhánh Parabol và gặp mặt đường tại B. Bom sẽ trúng xe khi bom và xe cùng lúc đến B.

\( \Rightarrow t = \sqrt {\frac{{2h}}{g}} \)

Lúc t = 0, xe tăng ở A: \(AB = {V_2}t = {V_2}\sqrt {\frac{{2h}}{g}} \)

Khoảng cách khi cắt bom là: \(HA = HB - AB = \left( {{V_1} - {V_2}} \right)\sqrt {\frac{{2h}}{g}} \)

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Dao động điều hoà có vận tốc cực đại là v_max = 8π cm/s và gia tốc cực đại a_max= 16π² cm/s² thì biên độ của dao động là

A. 3 cm.

B. 4 cm.

C. 5 cm.

D. 8 cm.

Lời giải

Ta có:

\(\left\{ \begin{array}{l}{v_{max}} = \omega A\\{a_{max}} = {\omega ^2}A\end{array} \right. \Rightarrow v_{max}^2 = {\omega ^2}{A^2} \Rightarrow \frac{{v_{max}^2}}{{{a_{max}}}} = A = 4\left( {cm} \right)\)

Đáp án đúng: B

Câu 2

Người ta đặt chìm trong nước một nguồn âm có tần số 725 Hz.Vận tốc truyền âm trong nước là 1450 m/s. Khoảng cách gần nhau nhất giữa hai điểm trong nước dao động ngược pha là

A. 2 m.

B. 1 m.

C. 1,2 m.

D. 2,4 m.

Lời giải

Ta có: \(v = \lambda .f \Rightarrow \lambda = \frac{v}{f} = 2\left( m \right)\)

Lại có khoảng cách giữa hai điểm gần nhau nhất dao động ngược pha là \[\frac{1}{2}\] bước sóng => d = 1 m.

Đáp án đúng: B

Câu 3

Một điện tích điểm q = -4.10^-8C di chuyển dọc theo chu vi của một tam giác MNP, vuông tại P, trong điện trường đều có cường độ 200 V/m. Cạnh MN = 10 cm, MN cùng phương cùng chiều với \(\vec E\). Cho NP = 8 cm. Môi trường là không khí. Tính công của lực điện trong các dịch chuyển sau của q:

a, từ M đến N.

b, từ N đến P.

c, từ P đến M.

d, theo đường kín MNPM.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Một vật dao động điều hoà theo phương trình x = 5cos(2πt - π/2) cm. Kể từ lúc t = 0, quãng đường vật đi được sau 12,375 s bằng

A. 235 cm.

B. 246,46 cm.

C. 245,46 cm.

D. 247,5 cm.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Một vật dao động điều hòa với phương trình \[x = Acos\left( {\frac{{2\pi }}{T}t + \frac{\pi }{2}} \right).\] Thời gian ngắn nhất kể từ lúc bắt đầu dao động tới khi vật có gia tốc bằng một nửa giá trị cực đại là

A. t = T/12.

B. t = T/6.

C. t = T/3.

D. t = 5T/12.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Chọn câu sai trong các phát biểu sau?

A. Nguyên tắc tạo ra dòng điện xoay chiều dựa trên hiện tượng cảm ứng điện từ.

B. Khi đo cường độ dòng điện xoay chiều, người ta có thể dùng ampe kế nhiệt.

C. Số chỉ của ampe kế xoay chiều cho biết giá trị hiệu dụng của dòng điện xoay chiều.

D. Giá trị hiệu dụng của dòng điện xoay chiều bằng giá trị trung bình của dòng điện xoay chiều.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Một con lắc đơn có chiều dài 70 cm đang dao động cưỡng bức với biên độ góc nhỏ, tại nơi có g = 10 m/s². Khi có cộng hưởng, con lắc dao động điều hòa với chu kì là

A. 1,66 s.

B. 0,60 s.

C. 0,76 s.

D. 1,04 s.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Dao động điều hoà có vận tốc cực đại là vmax = 8π cm/s và gia tốc cực đại amax= 16π2 cm/s2 thì biên độ của dao động là

Người ta đặt chìm trong nước một nguồn âm có tần số 725 Hz.Vận tốc truyền âm trong nước là 1450 m/s. Khoảng cách gần nhau nhất giữa hai điểm trong nước dao động ngược pha là

Một vật dao động điều hoà theo phương trình x = 5cos(2πt - π/2) cm. Kể từ lúc t = 0, quãng đường vật đi được sau 12,375 s bằng

Một vật dao động điều hòa với phương trình \[x = Acos\left( {\frac{{2\pi }}{T}t + \frac{\pi }{2}} \right).\] Thời gian ngắn nhất kể từ lúc bắt đầu dao động tới khi vật có gia tốc bằng một nửa giá trị cực đại là

Chọn câu sai trong các phát biểu sau?

Một con lắc đơn có chiều dài 70 cm đang dao động cưỡng bức với biên độ góc nhỏ, tại nơi có g = 10 m/s2. Khi có cộng hưởng, con lắc dao động điều hòa với chu kì là

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Dao động điều hoà có vận tốc cực đại là v_max = 8π cm/s và gia tốc cực đại a_max= 16π² cm/s² thì biên độ của dao động là

Một con lắc đơn có chiều dài 70 cm đang dao động cưỡng bức với biên độ góc nhỏ, tại nơi có g = 10 m/s². Khi có cộng hưởng, con lắc dao động điều hòa với chu kì là