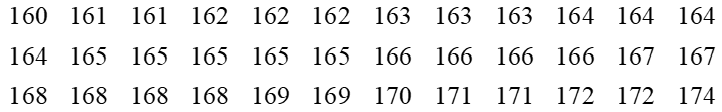Quan sát bảng tần số ghép nhóm bao gồm cả tần số tích luỹ ở Ví dụ 6 rồi cho biết:
Nhóm
Tần số
Tần số tích lũy
[30; 40)
[40; 50)
[50; 60)
[60; 70)
[70; 80)
[80; 90)
2
10
16
8
2
2
1
12
28
36
38
40
n = 40
Bảng 13
a) Nhóm nào có tần số lớn nhất;
b) Đầu mút trái và độ dài của nhóm có tần số lớn nhất bằng bao nhiêu.
Quan sát bảng tần số ghép nhóm bao gồm cả tần số tích luỹ ở Ví dụ 6 rồi cho biết:
|
Nhóm |
Tần số |
Tần số tích lũy |
|
[30; 40) [40; 50) [50; 60) [60; 70) [70; 80) [80; 90) |
2 10 16 8 2 2 |
1 12 28 36 38 40 |
|
|
n = 40 |
|
Bảng 13
a) Nhóm nào có tần số lớn nhất;
b) Đầu mút trái và độ dài của nhóm có tần số lớn nhất bằng bao nhiêu.
Quảng cáo
Trả lời:
Từ bảng tần số ghép nhóm và tần số tích lũy ta có:
a) Nhóm 3 là nhóm [50; 60) có tần số lớn nhất.
b) Nhóm [50; 60) có đầu mút trái là 50, độ dài là 10.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Sách - Sổ tay kiến thức trọng tâm Vật lí 11 VietJack - Sách 2025 theo chương trình mới cho 2k8 ( 45.000₫ )
- Trọng tâm Hóa học 11 dùng cho cả 3 bộ sách Kết nối, Cánh diều, Chân trời sáng tạo VietJack - Sách 2025 ( 58.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
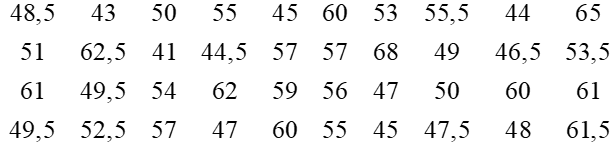
a) Bảng tần số ghép nhóm cho mẫu số liệu trên như sau:
|
Nhóm |
Tần số |
|
[40; 45) |
4 |
|
[45; 50) |
11 |
|
[50; 55) |
7 |
|
[55; 60) |
8 |
|
[60; 65) |
8 |
|
[65; 70) |
2 |
|
|
n = 40 |
Lời giải
a) Bảng tần số ghép nhóm bao gồm giá trị đại diện và tần số tích lũy như sau:
|
Nhóm |
Giá trị đại diện |
Tần số |
Tần số tích lũy |
|
[30; 40) |
35 |
4 |
4 |
|
[40; 50) |
45 |
10 |
14 |
|
[50; 60) |
55 |
14 |
28 |
|
[60; 70) |
65 |
6 |
34 |
|
[70; 80) |
75 |
4 |
38 |
|
[80; 90) |
85 |
2 |
40 |
|
|
|
n = 40 |
|
⦁ Số trung bình cộng của mẫu số liệu ghép nhóm đã cho là:
⦁ Số phần tử của mẫu là n = 40. Ta có
Mà 14 < 20 < 28 nên nhóm 3 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 20.
Xét nhóm 3 là nhóm [50; 60) có r = 50, d = 10, n3 = 14 và nhóm 2 là nhóm [40; 50) có cf2 = 14.
Áp dụng công thức, ta có trung vị của mẫu số liệu là:
(cm).
Do đó tứ phân vị thứ hai là Q2 = Me ≈ 54,29 (cm).
⦁ Ta có . Mà 4 < 10 < 14 nên nhóm 2 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 10.
Xét nhóm 2 là nhóm [40; 50) có s = 40; h = 10; n2 = 10 và nhóm 1 là nhóm [30; 40) có cf1 = 4.
Áp dụng công thức, ta có tứ phân vị thứ nhất là:
(cm).
⦁ Ta có Mà 28 < 30 < 34 nên nhóm 4 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 30.
Xét nhóm 4 là nhóm [60; 70) có t = 60; l = 10; n4 = 6 và nhóm 3 là nhóm [50; 60) có cf3 = 28.
Áp dụng công thức, ta có tứ phân vị thứ ba là:
(cm).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.