Câu hỏi:
13/07/2024 9,509
Trò chơi vòng quay may mắn.
Một bánh xe hình tròn được chia thành 12 hình quạt như nhau, trong đó có 2 hình quạt ghi 100 điểm, 2 hình quạt ghi 200 điểm, 2 hình quạt ghi 300 điểm, 2 hình quạt ghi 400 điểm, 1 hình quạt ghi 500 điểm, 2 hình quạt ghi 1 000 điểm, 1 hình quạt ghi 2000 điểm (H.8.3). Ở mỗi lượt, người chơi quay bánh xe. Mũi tên cố định gắn trên vành bánh xe dừng ở hình quạt nào thì người chơi nhận được số điểm ghi trên hình quạt đó.
Bạn Lan chơi trò chơi này. Tính xác suất của các biến cố sau:
a) A: "Trong một lượt quay, Lan quay được 400 điểm";
b) B: "Trong một lượt quay, Lan được ít nhất 500 điểm".
Trò chơi vòng quay may mắn.
Một bánh xe hình tròn được chia thành 12 hình quạt như nhau, trong đó có 2 hình quạt ghi 100 điểm, 2 hình quạt ghi 200 điểm, 2 hình quạt ghi 300 điểm, 2 hình quạt ghi 400 điểm, 1 hình quạt ghi 500 điểm, 2 hình quạt ghi 1 000 điểm, 1 hình quạt ghi 2000 điểm (H.8.3). Ở mỗi lượt, người chơi quay bánh xe. Mũi tên cố định gắn trên vành bánh xe dừng ở hình quạt nào thì người chơi nhận được số điểm ghi trên hình quạt đó.
Bạn Lan chơi trò chơi này. Tính xác suất của các biến cố sau:
a) A: "Trong một lượt quay, Lan quay được 400 điểm";
b) B: "Trong một lượt quay, Lan được ít nhất 500 điểm".
Quảng cáo
Trả lời:
Giải bởi Vietjack
Mũi tên có thể dừng ở 1 trong 12 hình quạt như nhau nên 12 kết quả có thể này là đồng khả năng.
a) Có 2 hình quạt ghi 400 điểm nên có 2 kết quả thuận lợi cho biến cố A.
Do đó, xác suất của biến cố A là
b) Lan quay được ít nhất 500 điểm, tức là Lan có thể quay được 500 điểm hoặc 1 000 điểm hoặc 2 000 điểm.
Có 1 hình quạt ghi 500 điểm, 2 hình quạt ghi 1 000 điểm, 1 hình quạt ghi 2 000 điểm nên có 1 + 2 + 1 = 4 kết quả thuận lợi cho biến cố B.
Do đó, xác suất của biến cố B là
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
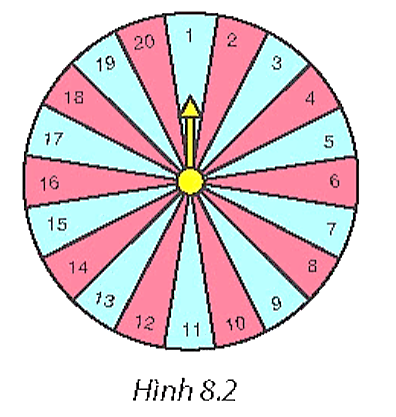
Có 20 kết quả có thể, đó là 1; 2;...; 20. Do 20 hình quạt như nhau nên 20 kết quả có thể này là đồng khả năng.
a) Từ 1 đến 20 có 4; 8; 12; 16; 20 chia hết cho 4, vậy có 5 hình quạt ghi số chia hết cho 4.
Gọi E là biến cố: “Mũi tên chỉ vào hình quạt ghi số chia hết cho 4”. Khi đó có 5 kết quả thuận lợi cho biến cố E.
Vậy xác suất để mũi tên chỉ vào hình quạt ghi số chia hết cho 4 là:
b) Có số 1; 4; 6; 8; 9; 10; 12; 14; 15; 16; 18; 20 không phải số nguyên tố, vậy có 12 hình quạt ghi số không phải là số nguyên tố.
Gọi F là biến cố: “Mũi tên chỉ vào hình quạt ghi số không phải là số nguyên tố”. Khi đó có 12 kết quả thuận lợi cho biến cố F.
Vậy xác suất để mũi tên chỉ vào hình quạt ghi số không phải là số nguyên tố là:
Lời giải
Gọi số lượng cuốn tiểu thuyết ban đầu là x (cuốn).
Số lượng cuốn tiểu thuyết khi đặt thêm 5 cuốn tiểu thuyết mới mua là x + 5 (cuốn).
Theo đề bài ta có: , tức là 4(x + 5) = 60 hay x + 5 = 15, suy x = 10.
Vậy ban đầu có 10 cuốn tiểu thuyết.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
15 câu Trắc nghiệm Toán 8 Kết nối tri thức Bài 1: Đơn thức có đáp án
-
Dạng 1: Bài luyện tập 1 dạng 1: Tính có đáp án
-
Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 24
-
Bộ 10 đề thi giữa kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 1
-
Đề cuối kì 2 Toán 8 Chân trời sáng tạo cấu trúc mới có đáp án - Đề 1
-
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 2)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận