Cho a, b, c là ba số thực dương, a > 1 thỏa mãn loga2(bc)+logab3c3+bc42+4+9−c2=0 Khi đó, giá trị của biểu thức T = a + 3b + 2c gần với giá nào nhất sau đây? A. 8. B. 9. C. 7. D. 10.

Áp dụng bất đẳng thức (x+y)2≥4xy, ta được b3c3+bc42≥b4c4⇒logab3c3+bc42≥4loga(bc). Do đó với ∀a>1,b,c>0 loga2(bc)+logab3c3+bc42+4+9−c2≥loga2(bc)+4loga(bc)+4+9−c2 ⇔loga2(bc)+logab3c3+bc42+4+9−c2≥loga(bc)+22+9−c2≥0. Dấu “=” xảy ra khi b3c3=bc4loga(bc)=−2c2=9a>1b>0c>0⇒a=2b=16c=3. Khi đó T=a+3b+2c=2+12+6≈7,91. Vậy giá trị của T gần 8 nhất. Chọn A

Câu hỏi:

10/12/2023 118

Cho a, b, c là ba số thực dương, a > 1 thỏa mãn

$\log_{a}^{2} (b c) + \log_{a} {(b^{3} c^{3} + \frac{b c}{4})}^{2} + 4 + \sqrt{9 - c^{2}} = 0$

Khi đó, giá trị của biểu thức T = a + 3b + 2c gần với giá nào nhất sau đây?

A. 8.

B. 9.

C. 7.

D. 10.

Xem lời giải

Câu hỏi trong đề: Đề thi Đánh giá tư duy tốc chiến Đại học Bách khoa năm 2023-2024 có đáp án (Đề 8) !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Áp dụng bất đẳng thức ${(x + y)}^{2} \geq 4 x y,$ ta được

${(b^{3} c^{3} + \frac{b c}{4})}^{2} \geq b^{4} c^{4} \Rightarrow \log_{a} {(b^{3} c^{3} + \frac{b c}{4})}^{2} \geq 4 \log_{a} (b c) .$

Do đó với $\forall a > 1, b, c > 0$

$\log_{a}^{2} (b c) + \log_{a} {(b^{3} c^{3} + \frac{b c}{4})}^{2} + 4 + \sqrt{9 - c^{2}} \geq \log_{a}^{2} (b c) + 4 \log_{a} (b c) + 4 + \sqrt{9 - c^{2}}$

$\Leftrightarrow \log_{a}^{2} (b c) + \log_{a} {(b^{3} c^{3} + \frac{b c}{4})}^{2} + 4 + \sqrt{9 - c^{2}} \geq {[\log_{a} (b c) + 2]}^{2} + \sqrt{9 - c^{2}} \geq 0.$

Dấu “=” xảy ra khi $\{\begin{array}{l} b^{3} c^{3} = \frac{b c}{4} \\ \log_{a} (b c) = - 2 \\ c^{2} = 9 \\ a > 1 \\ b > 0 \\ c > 0 \end{array} \Rightarrow \{\begin{cases} a = \sqrt{2} \\ b = \frac{1}{6} \\ c = 3 \end{cases} .$

Khi đó $T = a + 3 b + 2 c = \sqrt{2} + \frac{1}{2} + 6 \approx 7, 91.$ Vậy giá trị của T gần 8 nhất.

Chọn A

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Một ô tô bắt đầu chuyển động nhanh dần đều với vận tốc v₁(t) = 2t (m/s). Đi được 12 giây, người lái xe phát hiện chướng ngại vật và phanh gấp, ô tô tiếp tục chuyển động chậm dần đều với gia tốc
a = −12 (m/s²). Tính quãng đường s(m) đi được của ô tô từ lúc bắt đầu chuyển bánh cho đến khi dừng hẳn

A. s = 168 m.

B. s = 166 m.

C. s = 144 m.

D. s = 152 m.

Lời giải

Quãng đường xe đi được trong 12s đầu là: $s_{1} = \int_{0}^{12} 2 t d t = 144 m .$

Sau khi đi được 12s ô tô đạt vận tốc v= 24m/s sau đó vận tốc của ô tô có phương trình $v = 24 - 12 t .$ Xe dừng hẳn sau 2s kể từ khi phanh.

Quãng đường ô tô đi được từ khi đạp phanh đến khi dừng hẳn là: $s_{2} = \int_{0}^{2} (24 - 12 t) d t = 24 m .$

Vậy tổng quãng đường 0 tô đi được là $s = s_{1} + s_{2} = 144 + 24 = 168 m.$

Chọn A

Câu 2

Cho hình chóp SABCD có đáy là hình chữ nhật, AB = 2a, AD = a; tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy. Góc $α$ tạo bởi hai mặt phẳng (SCD) và (ABCD) có số đo bằng

α

= 90°.

α

= 30°.

α

= 60°.

α

= 45°.

Lời giải

+) Gọi H là trung điểm AB, do tam giác SAB đều nên $S H ⊥ A B .$ Mà $(S A B) ⊥ (A B C D)$ nên $S H ⊥ (A B C D) .$

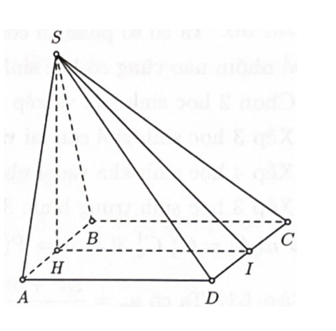
Cho hình chóp SABCD có đáy là hình chữ nhật, AB = 2a, AD = a; tam giác SAB đều và nằm trong mặt phẳng vuông góc (ảnh 1)

+) Gọi I là trung điểm CD.

Ta có: $α = ((S C D); (A B C D)) = \hat{S I H} .$

+) Trong đó: SH là đường cao của tam giác đều cạnh 2a nên $S H = a \sqrt{3}, H I = A D = a .$

+) Khi đó $\tan α = \tan \hat{S I H} = \frac{S H}{H I} = \sqrt{3},$ suy ra $α = 60 ° .$

Chọn C

Câu 3

Hình elip được ứng dụng nhiều trong thực tiễn, đặc biệt là kiến trúc xây dựng như đấu trường La Mã, tòa nhà Ellipse Tower Hà Nội, sử dụng trong thiết kế logo quảng cáo, thiết bị nội thất,... Xét một Lavabo làm bằng sứ đặc hình dạng là một nửa khối elip tròn xoay có thông số kĩ thuật mặt trên của Lavabo dài × rộng là 660 × 380 mm. Biết rằng Lavabo có độ dày đều là 20 mm.

Thể tích chứa nước của Lavabo gần với giá trị nào trong các giá trị sau.

A. 18,66 dm³.

B. 18,76 dm³.

C. 18,86 dm³.

D. 18,96 dm³.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Từ 12 học sinh gồm 5 học sinh giỏi, 4 học sinh khá, 3 học sinh trung bình, giáo viên muốn thành lập 4 nhóm làm 4 bài tập lớn khác nhau, mỗi nhóm 3 học sinh. Tính xác suất để nhóm nào cũng có học sinh giỏi và học sinh khá.

\frac{36}{285} .

\frac{18}{285} .

\frac{72}{285} .

\frac{144}{285} .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Ý nào sau đây thể hiện rõ nhất nội dung chính của bài đọc trên?

A. Sử dụng công nghệ sinh học để sản xuất trầm hương nhân tạo.

B. Tình hình nghiên cứu và sản xuất trầm hương ở Việt Nam hiện nay.

C. Những ưu điểm của trầm hương nhân tạo so với trầm hương tự nhiên.

D. Hợp tác khoa học quốc tế trong lĩnh vực sản xuất trầm hương.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Hình vẽ bên là đồ thị của hàm số $y = \frac{a x + b}{c x + d} (a b - b c \neq 0) .$ Mệnh đề nào sau đây là đúng?

A. bd > 0, ad > 0.

B. bd < 0, ab > 0.

C. ad > 0, ab < 0.

D. ab < 0, ad < 0.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Ý nào sau đây thể hiện rõ nhất nội dung chính của bài đọc trên?

A. Giới thiệu công ty cổ phần Ong Tam Đảo (Honeco).

B. Giới thiệu các công dụng của mật ong và hoa quả với sức khỏe.

C. Giới thiệu công nghệ cô đặc chân không áp dụng với mật ong.

D. Giới thiệu nghiên cứu sản xuất sản phẩm từ mật ong và hoa quả.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Cho a, b, c là ba số thực dương, a > 1 thỏa mãn loga2(bc)+logab3c3+bc42+4+9−c2=0 Khi đó, giá trị của biểu thức T = a + 3b + 2c gần với giá nào nhất sau đây?

Cho hình chóp SABCD có đáy là hình chữ nhật, AB = 2a, AD = a; tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy. Góc α tạo bởi hai mặt phẳng (SCD) và (ABCD) có số đo bằng

Từ 12 học sinh gồm 5 học sinh giỏi, 4 học sinh khá, 3 học sinh trung bình, giáo viên muốn thành lập 4 nhóm làm 4 bài tập lớn khác nhau, mỗi nhóm 3 học sinh. Tính xác suất để nhóm nào cũng có học sinh giỏi và học sinh khá.

Ý nào sau đây thể hiện rõ nhất nội dung chính của bài đọc trên?

Hình vẽ bên là đồ thị của hàm số y=ax+bcx+d(ab−bc≠0). Mệnh đề nào sau đây là đúng?

Ý nào sau đây thể hiện rõ nhất nội dung chính của bài đọc trên?

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Cho a, b, c là ba số thực dương, a > 1 thỏa mãn

$\log_{a}^{2} (b c) + \log_{a} {(b^{3} c^{3} + \frac{b c}{4})}^{2} + 4 + \sqrt{9 - c^{2}} = 0$

Khi đó, giá trị của biểu thức T = a + 3b + 2c gần với giá nào nhất sau đây?

Cho hình chóp SABCD có đáy là hình chữ nhật, AB = 2a, AD = a; tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy. Góc $α$ tạo bởi hai mặt phẳng (SCD) và (ABCD) có số đo bằng

Hình vẽ bên là đồ thị của hàm số $y = \frac{a x + b}{c x + d} (a b - b c \neq 0) .$ Mệnh đề nào sau đây là đúng?