Câu hỏi:
13/07/2024 322
Trong tháng vừa qua có 3 084 người nhập cảnh ngắn hạn vào nước X. Cơ quan hải quan thống kê mục đích nhập cảnh của họ và cho kết quả trong bảng sau:
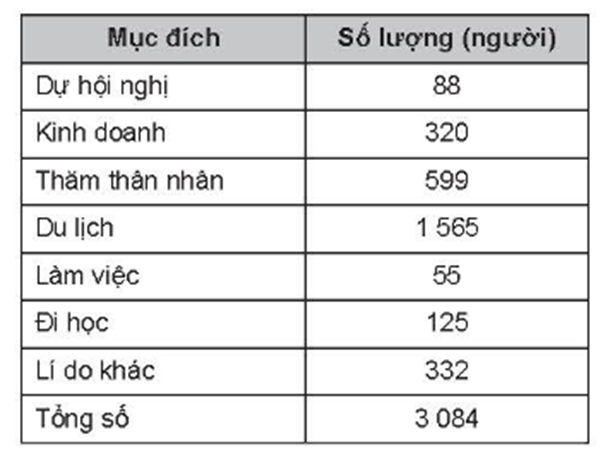
Tính xác suất thực nghiệm để người nhập cảnh ngắn hạn vào nước X tháng qua (biểu diễn bằng phần trăm) với mục đích:
+ Kinh doanh;
+ Du lịch;
+ Làm việc hoặc đi học;
+ Kinh doanh hoặc dự hội nghị.
Trong tháng vừa qua có 3 084 người nhập cảnh ngắn hạn vào nước X. Cơ quan hải quan thống kê mục đích nhập cảnh của họ và cho kết quả trong bảng sau:
Tính xác suất thực nghiệm để người nhập cảnh ngắn hạn vào nước X tháng qua (biểu diễn bằng phần trăm) với mục đích:
+ Kinh doanh;
+ Du lịch;
+ Làm việc hoặc đi học;
+ Kinh doanh hoặc dự hội nghị.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Trong 3 084 người nhập cảnh ngắn hạn vào nước X trong tháng qua thì có 320 người nhập cảnh với mục đích kinh doanh. Vậy xác suất thực nghiệm để người nhập cảnh ngắn hạn vào nước X tháng qua với mục đích kinh doanh là: \(\frac{{320}}{{3084}} \approx 10,38\% \).
Trong 3 084 người nhập cảnh ngắn hạn vào nước X trong tháng qua thì có 1 565 người nhập cảnh với mục đích du lịch. Vậy xác suất thực nghiệm để người nhập cảnh ngắn hạn vào nước X tháng qua với mục đích du lịch là: \(\frac{{1565}}{{3084}} \approx 50,75\% \).
Trong 3 084 người nhập cảnh ngắn hạn vào nước X trong tháng qua thì có 55 người nhập cảnh với mục đích làm việc và 125 người nhập cảnh với mục đích đi học. Xác suất thực nghiệm để người nhập cảnh ngắn hạn vào nước X tháng qua với mục đích làm việc hoặc đi học là: \(\frac{{55 + 125}}{{3084}} = \frac{{180}}{{3084}} \approx 5,84\% \).
Trong 3 084 người nhập cảnh ngắn hạn vào nước X trong tháng qua thì có 320 người nhập cảnh với mục đích kinh doanh và 88 người nhập cảnh với mục đích dự hội nghị. Xác suất thực nghiệm để người nhập cảnh ngắn hạn vào nước X tháng qua với mục đích kinh doanh hoặc dự hội nghị là: \(\frac{{320 + 88}}{{3084}} \approx 13,23\% \).
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi k là số ngày trong 100 ngày ghi nhận tắc đường vào giờ cao điểm buổi sáng tại đường X.
Do trong 365 ngày liên tiếp ghi nhận 217 ngày bị tắc đường vào giờ cao điểm buổi sáng nên ta có: \(\frac{k}{{100}} \approx \frac{{217}}{{365}}\).
Suy ra: k ≈ \(\frac{{100 \cdot 217}}{{365}} \approx \) 59,452.
Vậy ta dự đoán trong 100 ngày tới có khoảng 59 ngày tắc đường trong giờ cao điểm tại đường X.
Lời giải
Tổng số vụ tai nạn là 1 830.
Số vụ tai nạn khi đi xe máy hoặc xe đạp là: 1 354 + 55 = 1 409.
Do đó xác suất thực nghiệm của biến cố F là \(\frac{{1409}}{{1830}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
15 câu Trắc nghiệm Toán 8 Kết nối tri thức Bài 1: Đơn thức có đáp án
-
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 24
-
Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 1
-
Bộ 10 đề thi giữa kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
Đề cuối kì 2 Toán 8 Chân trời sáng tạo cấu trúc mới có đáp án - Đề 1
-
15 câu Trắc nghiệm Toán 8 Cánh diều Bài 1: Đơn thức nhiều biến. Đa thức nhiều biến có đáp án
-
15 câu Trắc nghiệm Toán 8 Chân trời sáng tạo Bài 1: Đơn thức và đa thức nhiều biến có đáp án
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận