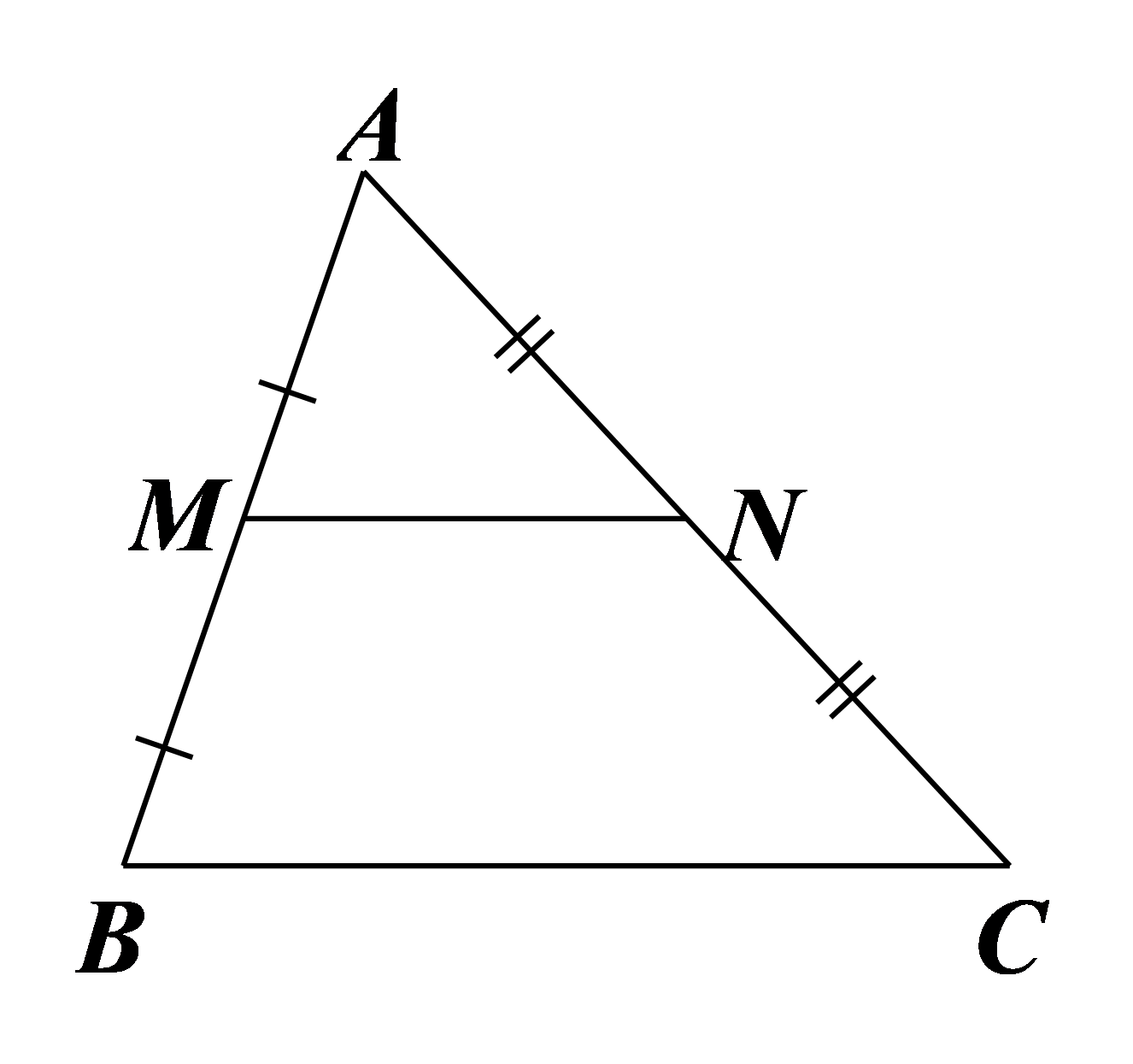Cho tam giác ABC có và Gọi I và G lần lượt là tâm đường tròn nội tiếp và trọng tâm
a) Tính độ dài các đoạn thẳng CD và BD.
b) Chứng minh
c) Tính độ dài đoạn thẳng IG.
Cho tam giác ABC có và Gọi I và G lần lượt là tâm đường tròn nội tiếp và trọng tâm
a) Tính độ dài các đoạn thẳng CD và BD.
b) Chứng minh
c) Tính độ dài đoạn thẳng IG.
Câu hỏi trong đề: Đề kiểm tra Giữa kì 2 Toán 8 CTST có đáp án !!
Quảng cáo
Trả lời:
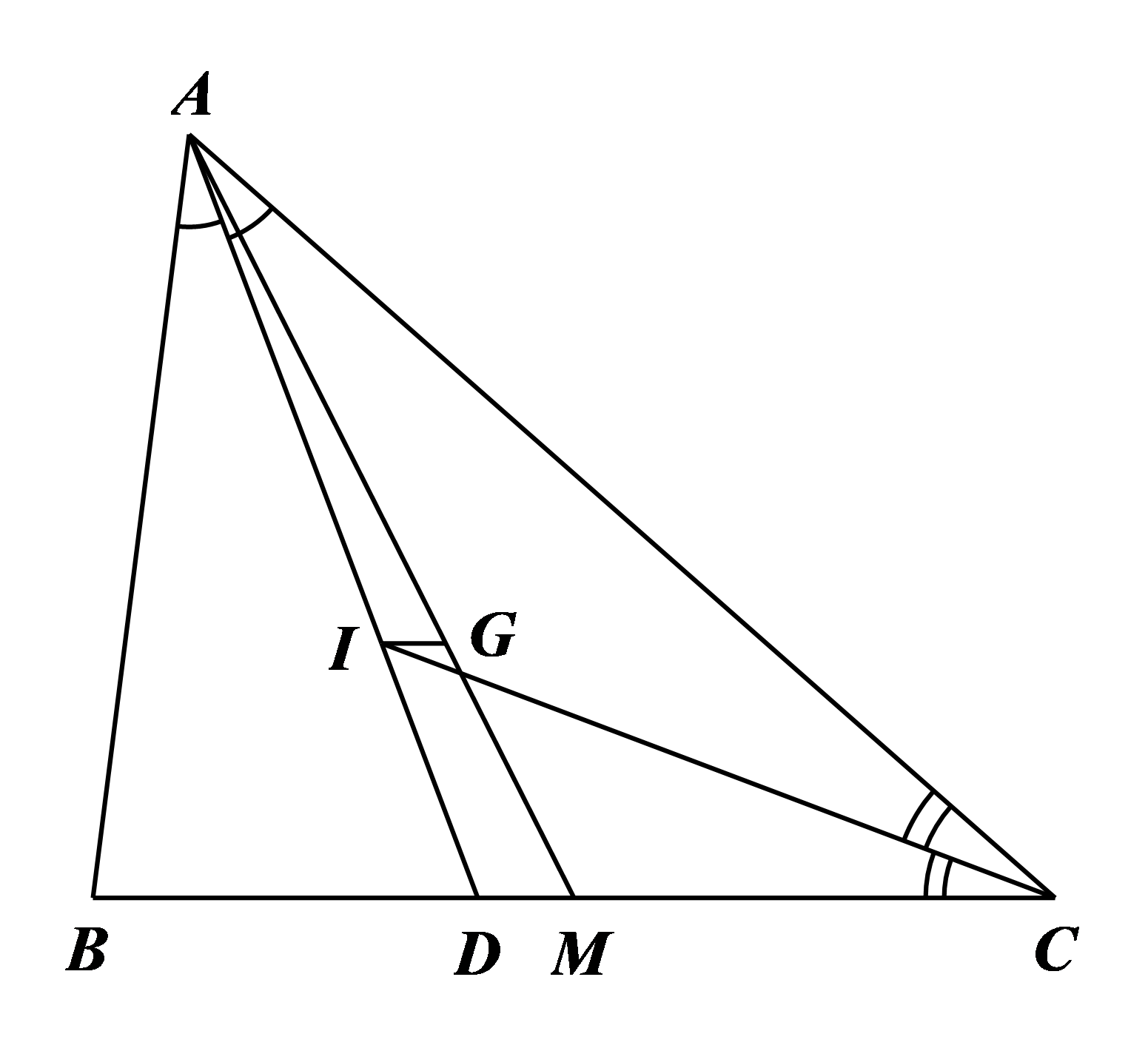
a) Gọi AD là đường phân giác góc BAC
Xét có AD là đường phân giác của nên hay
Theo tính chất dãy tỉ số bằng nhau ta có:
Suy ra và
b) Xét có CI là đường phân giác của nên
Mặt khác, do G là trọng tâm của nên
Do đó theo định lí Thalès đảo ta có
c) Gọi M là trung điểm của BC. Khi đó
Suy ra
Xét có theo hệ quả định lí Thalès ta có
Suy ra
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Với để đường thẳng song song với đường thẳng thì và tức là (thỏa mãn
Vậy m = 3
b) ⦁ Với m = 3 ta có hàm số
Cho x = 0 ta có y = 3
Cho x = -1 ta có y = 1
Đồ thị hàm số là đường thẳng (d) đi qua hai điểm (0;3) và (-1;1)
⦁ Xét hàm số
Cho x = 0 ta có y = -3
Cho x = 1 ta có y = -1
Đồ thị hàm số là đường thẳng (d') đi qua hai điểm (0;-3) và (1;-1)

c) Gọi là giao điểm của hai đường thẳng
Vì A thuộc đường thẳng y = x + 2 nên ta có Khi đó
Vì A thuộc đường thẳng nên ta có suy ra do đó
Từ đó ta có
Vì vậy ta được
Để ba đường thẳng và đồng quy thì đường thẳng (d) phải đi qua giao điểm A(2;4) của hai đường thẳng
Khi đó thỏa mãn hàm số ta được:
suy ra do đó 3m = 6 nên m = 2 (thỏa mãn
Vậy m = 2.
Lời giải
Chọn đáp án B
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. 1,5 cm
B. 3 cm
C. 4,5 cm
D. 6 cm
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. là đường trung tuyến của
B. là đường trung bình của
C. là đường trung trực của
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
D. Cả A, B, C đều sai.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.