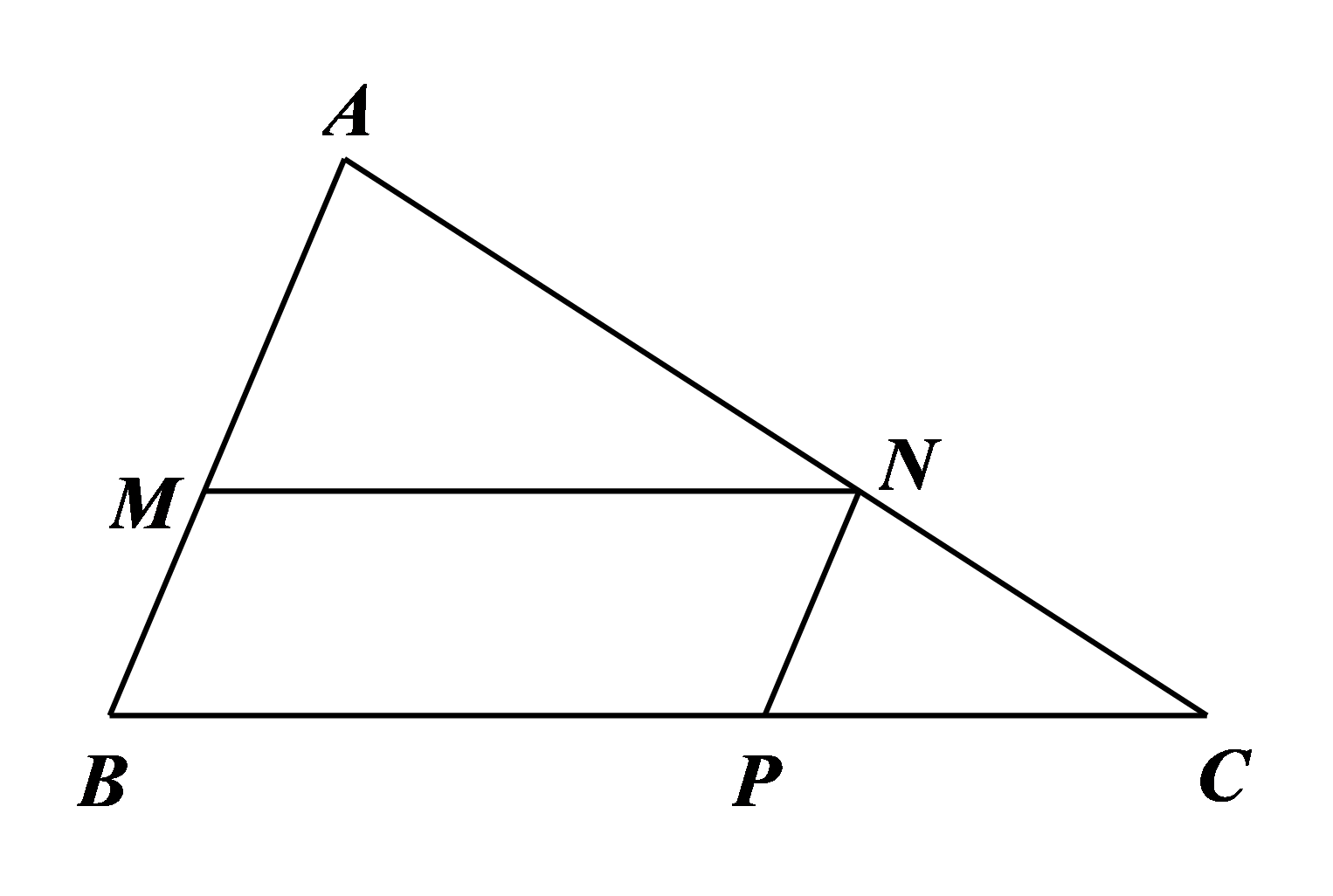Câu hỏi:
07/03/2024 533
Cho cân tại A đường trung tuyến AH Gọi I và K lần lượt là trung điểm của AC và AB Gọi E là điểm sao cho I là trung điểm của HE.
a) Giải thích tại sao tứ giác AKHI là hình thoi.
Cho cân tại A đường trung tuyến AH Gọi I và K lần lượt là trung điểm của AC và AB Gọi E là điểm sao cho I là trung điểm của HE.
a) Giải thích tại sao tứ giác AKHI là hình thoi.
Câu hỏi trong đề: Đề kiểm tra Cuối kì 1 Toán 8 KNTT có đáp án !!
Bắt đầu thiQuảng cáo
Trả lời:
Giải bởi Vietjack
a) Xét cân tại A có AH là đường trung tuyến nên đồng thời là đường cao của tam giác.
Do đó nên và đều vuông tại 
Xét vuông tại H có HK là đường trung tuyến ứng với cạnh huyền AB nên (tính chất đường trung tuyến ứng với cạnh huyền của tam giác vuông).
Tương tự, xét vuông tại H ta có
Mà I, K lần lượt là trung điểm của AC và AB nên
Lại có AB = AC (do cân tại A)
Do đó
Xét tứ giác AKHI có nên là hình thoiCâu hỏi cùng đoạn
Câu 2:
b) Chứng minh rằng AHCE là hình chữ nhật. Tam giác ABC cần thêm điều kiện gì để tứ giác AHCE là hình vuông?
b) Chứng minh rằng AHCE là hình chữ nhật. Tam giác ABC cần thêm điều kiện gì để tứ giác AHCE là hình vuông?
Lời giải của GV VietJack
b) Xét tứ giác AHCE có I là trung điểm của hai đường chéo AC, HE nên AHCE là hình bình hành.
Lại có nên hình bình hành AHCE là hình chữ nhật.
Để hình chữ nhật AHCE là hình vuông thì hai cạnh kề bằng nhau, tức HA = HC.
Mà H là trung điểm của BC nên
Khi đó
Xét có đường trung tuyến AH thỏa mãn nên vuông tại A
Vậy vuông cân tại A thì AHCE là hình vuông.
Nhà sách vietjack
Hot: Đề thi cuối kì 2 Toán, Văn, Anh.... file word có đáp án chi tiết lớp 1-12 form 2025 (chỉ từ 100k). Tải ngay
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Trong các dãy dữ liệu sau đây, dữ liệu nào là số liệu liên tục?
Xem đáp án »
07/03/2024
3,679
Câu 2:
Cho ba số thực a, b, c khác 2 và thỏa mãn a + b + c = 6 Tính giá trị của biểu thức:
Cho ba số thực a, b, c khác 2 và thỏa mãn a + b + c = 6 Tính giá trị của biểu thức:
Xem đáp án »
12/07/2024
3,169
Câu 4:
Chị Lan đã ghi lại khối lượng bán được của mỗi loại mà sạp hoa quả của chị bán được trong ngày và biểu diễn trong biểu đồ dưới đây:
a) Chị Lan đã thu thập dữ liệu được biểu diễn trên biểu đồ bằng phương pháp thu thập trực tiếp hay gián tiếp?
b) Hãy chuyển đổi dữ liệu từ biểu đồ trên sang dạng bảng thống kê theo mẫu sau:
Loại trái cây
Tỉ lệ phần trăm
Cam
?
Xoài
?
Mít
?
Ổi
?
Sầu riêng
?
c) Cho biết chị Lan bán được tổng cộng 200 kg trái cây trong ngày hôm đó. Hãy tính số kilôgam sầu riêng mà sạp hoa quả của chị Lan đã bán được trong ngày ấy.
Chị Lan đã ghi lại khối lượng bán được của mỗi loại mà sạp hoa quả của chị bán được trong ngày và biểu diễn trong biểu đồ dưới đây:
a) Chị Lan đã thu thập dữ liệu được biểu diễn trên biểu đồ bằng phương pháp thu thập trực tiếp hay gián tiếp?
b) Hãy chuyển đổi dữ liệu từ biểu đồ trên sang dạng bảng thống kê theo mẫu sau:
|
Loại trái cây |
Tỉ lệ phần trăm |
|
Cam |
? |
|
Xoài |
? |
|
Mít |
? |
|
Ổi |
? |
|
Sầu riêng |
? |
c) Cho biết chị Lan bán được tổng cộng 200 kg trái cây trong ngày hôm đó. Hãy tính số kilôgam sầu riêng mà sạp hoa quả của chị Lan đã bán được trong ngày ấy.
Xem đáp án »
07/03/2024
1,253
🔥 Đề thi HOT:
-
Đề kiểm tra Cuối kì 1 Toán 8 KNTT có đáp án (Đề 1)
-
Bộ 5 đề thi giữa kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
10 Bài tập Bài toán thực tiễn gắn với việc vận dụng định lí Thalès (có lời giải)
-
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
15 câu Trắc nghiệm Toán 8 Kết nối tri thức Bài 1: Đơn thức có đáp án
-
Bộ 10 đề thi giữa kì 2 Toán 8 Cánh diều cấu trúc mới có đáp án (Đề 1)
-
10 Bài tập Các bài toán thực tiễn gắn với việc vận dụng định lí Pythagore (có lời giải)
-
10 Bài tập Nhận biết hai hình đồng dạng, hai hình đồng dạng phối cảnh (có lời giải)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận