Câu hỏi:
12/07/2024 25,077
Cho tam giác ABC có ba góc nhọn (AB < AC). Kẻ đường cao BE, AK và CF cắt nhau tại H.
a) Chứng minh: .
b) Chứng minh: .
Cho tam giác ABC có ba góc nhọn (AB < AC). Kẻ đường cao BE, AK và CF cắt nhau tại H.
a) Chứng minh: .
b) Chứng minh: .
Câu hỏi trong đề:
Đề kiểm tra Cuối kì 2 Toán 8 CTST có đáp án !!
Sách mới 2k7: Tổng ôn Toán, Lí, Hóa, Văn, Sử, Địa…. kỳ thi tốt nghiệp THPT Quốc gia 2025, đánh giá năng lực (chỉ từ 110k).
Quảng cáo
Trả lời:
Giải bởi Vietjack
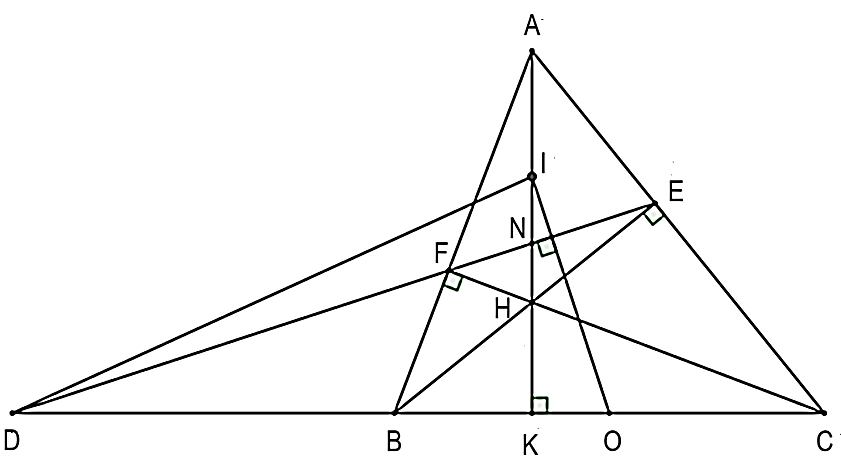
a) Xét và có:
Do đó .
b) Xét và có:
Do đó
Suy ra hay (đpcm)
Câu hỏi cùng đoạn
Câu 2:
c) Gọi N là giao điểm của AK và EF, D là giao điểm của đường thẳng BC và đường thẳng EF và O, I lần lượt là trung điểm của BC và AH. Chứng minh ON vuông góc DI.
c) Gọi N là giao điểm của AK và EF, D là giao điểm của đường thẳng BC và đường thẳng EF và O, I lần lượt là trung điểm của BC và AH. Chứng minh ON vuông góc DI.
Lời giải của GV VietJack
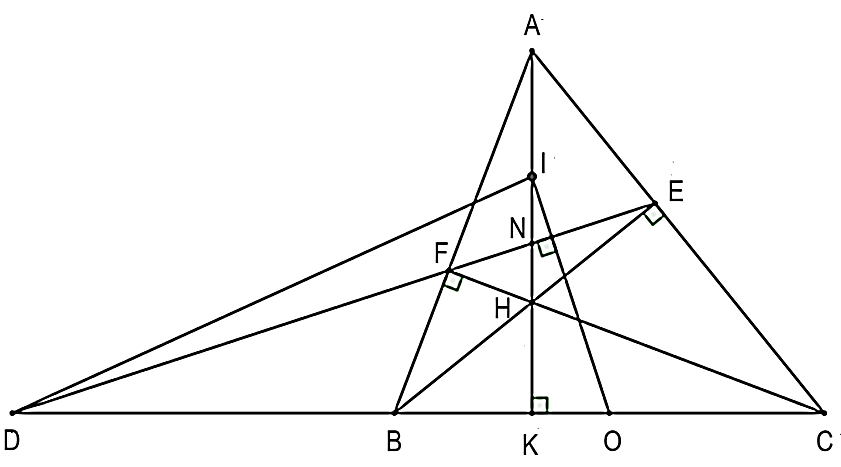
c)
• Xét vuông tại F có O là trung điểm của BC nên (1)
• Xét vuông tại E có O là trung điểm của BC nên (2)
Từ (1) và (2) nên suy ra (5)
• Xét vuông tại E có I là trung điểm của AH nên (3)
• Xét vuông tại F có I là trung điểm của AH nên (4)
Từ (3) và (4) nên suy ra (6)
Từ (5) và (6) ta suy ra được OI là đường trung trực của cạnh EF .
Khi đó hay .
Do đó DN là đường cao của .
Xét có DN và IK là đường cao và N là giao của DN và IK .
Do đó N là trực tâm của tam giác DOI .
Vậy (đpcm).
Nhà sách VIETJACK:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Viết ngẫu nhiên một số tự nhiên có hai chữ số nhỏ hơn 200.
a) Có bao nhiêu cách viết ngẫu nhiên một số tự nhiên như vậy?
b) Tính xác suất của mỗi biến cố “Số tự nhiên được viết ra là số tròn trăm”.
Viết ngẫu nhiên một số tự nhiên có hai chữ số nhỏ hơn 200.
a) Có bao nhiêu cách viết ngẫu nhiên một số tự nhiên như vậy?
b) Tính xác suất của mỗi biến cố “Số tự nhiên được viết ra là số tròn trăm”.
Xem đáp án »
12/07/2024
26,324
Câu 2:
Đường sông từ A đến B ngắn hơn đường bộ là 10 km. Ca nô đi từ A đến B mất 2 giờ 20 phút, ô tô đi hết 2 giờ. Vận tốc ca nô nhỏ hơn vận tốc ô tô là 17 km/h
Đường sông từ A đến B ngắn hơn đường bộ là 10 km. Ca nô đi từ A đến B mất 2 giờ 20 phút, ô tô đi hết 2 giờ. Vận tốc ca nô nhỏ hơn vận tốc ô tô là 17 km/h
Xem đáp án »
12/07/2024
9,277
Câu 3:
Để thiết kế mặt tiền cho căn nhà cấp bốn mái thái, sau khi xác định chiều dài mái PQ = 1,5 m. Chú thợ nhẩm tính chiều dài mái DE biết Q là trung điểm EC, P là trung điểm của DC. Tính giúp chú thợ xem chiều dài mái DE bằng bao nhiêu (xem hình vẽ minh họa)?
Để thiết kế mặt tiền cho căn nhà cấp bốn mái thái, sau khi xác định chiều dài mái PQ = 1,5 m. Chú thợ nhẩm tính chiều dài mái DE biết Q là trung điểm EC, P là trung điểm của DC. Tính giúp chú thợ xem chiều dài mái DE bằng bao nhiêu (xem hình vẽ minh họa)?
Xem đáp án »
12/07/2024
3,513
Câu 5:
Cho hàm số được xác định bởi công thức y = ax – 1. Biết đồ thị hàm số này đi qua điểm (1;2) Hoành độ của điểm thuộc đồ thị hàm số có tung độ bằng –4 là
Cho hàm số được xác định bởi công thức y = ax – 1. Biết đồ thị hàm số này đi qua điểm (1;2) Hoành độ của điểm thuộc đồ thị hàm số có tung độ bằng –4 là
Xem đáp án »
08/03/2024
2,675
Bình luận
🔥 Đề thi HOT:
-
10 Bài tập Bài toán thực tiễn gắn với việc vận dụng định lí Thalès (có lời giải)
-
10 Bài tập Các bài toán thực tiễn gắn với việc vận dụng định lí Pythagore (có lời giải)
-
15 câu Trắc nghiệm Toán 8 KNTT Bài 1: Đơn thức có đáp án
-
Bài tập Nhân đơn thức với đa thức (có lời giải chi tiết)
-
Đề kiểm tra Cuối kì 1 Toán 8 KNTT có đáp án (Đề 1)
-
10 Bài tập Các bài toán thực tiễn gắn với việc vận dụng định lí Pythagore (có lời giải)
-
10 Bài tập Bài toán thực tiễn gắn với việc vận dụng định lí Thalès (có lời giải)
-
10 Bài tập Bài toán thực tiễn liên quan đến thể tích, diện tích xung quanh của hình chóp tứ giác đều (có lời giải)
về câu hỏi!