Đọc văn bản và trả lời câu hỏi từ 32 đến 36.
Để dẫn điện từ nhà máy phát điện đến hộ tiêu thụ cần phải có đường dây tải điện. Nếu khoảng cách từ nơi sản xuất điện đến hộ tiêu thụ lớn, một vấn đề đặt ra là việc truyền tải điện năng đi xa làm sao cho kinh tế nhất.
Cùng một công suất truyền tải trên đường dây, nếu điện áp truyền tải cao thì dòng điện chạy trên đường dây nhỏ, do đó trọng lượng và chi phí dây dẫn sẽ giảm xuống, đồng thời tổn hao năng lượng trên đường dây sẽ giảm. Vì thế, muốn truyền tải công suất lớn đi xa ít tổn hao và tiết kiệm kim loại màu, người ta phải dùng điện áp cao, thường là 35, 110, 220, 500 kV. Thực tế các máy phát điện chỉ phát ra điện áp trong khoảng 3 - 21 kV, do đó phải có thiết bị tăng điện áp ở đầu đường dây. Mặt khác các hộ tiêu thụ thường yêu cầu điện áp thấp, từ 0,4 - 6 kV, vì vậy cuối đường dây phải có thiết bị giảm điện áp xuống. Thiết bị dùng để tăng điện áp ở đầu đường dây và giảm điện áp cuối đường dây gọi là máy biến áp.

Máy biến áp
Máy biến áp được dùng để
Đọc văn bản và trả lời câu hỏi từ 32 đến 36.
Để dẫn điện từ nhà máy phát điện đến hộ tiêu thụ cần phải có đường dây tải điện. Nếu khoảng cách từ nơi sản xuất điện đến hộ tiêu thụ lớn, một vấn đề đặt ra là việc truyền tải điện năng đi xa làm sao cho kinh tế nhất.
Cùng một công suất truyền tải trên đường dây, nếu điện áp truyền tải cao thì dòng điện chạy trên đường dây nhỏ, do đó trọng lượng và chi phí dây dẫn sẽ giảm xuống, đồng thời tổn hao năng lượng trên đường dây sẽ giảm. Vì thế, muốn truyền tải công suất lớn đi xa ít tổn hao và tiết kiệm kim loại màu, người ta phải dùng điện áp cao, thường là 35, 110, 220, 500 kV. Thực tế các máy phát điện chỉ phát ra điện áp trong khoảng 3 - 21 kV, do đó phải có thiết bị tăng điện áp ở đầu đường dây. Mặt khác các hộ tiêu thụ thường yêu cầu điện áp thấp, từ 0,4 - 6 kV, vì vậy cuối đường dây phải có thiết bị giảm điện áp xuống. Thiết bị dùng để tăng điện áp ở đầu đường dây và giảm điện áp cuối đường dây gọi là máy biến áp.

Máy biến áp
Máy biến áp được dùng để
A. biến đổi tần số của dòng điện xoay chiều.
B. biến đổi cường độ của dòng điện xoay chiều.
C. biến đổi công suất của dòng điện xoay chiều.
Quảng cáo
Trả lời:
Chọn đáp án D
Câu hỏi cùng đoạn
Câu 2:
Máy biến áp hoạt động dựa vào hiện tượng
Chọn D
Câu 3:
Một máy biến áp có số vòng dây cuộn sơ cấp lớn hơn số vòng dây của cuộn thứ cấp. Máy biến áp này có tác dụng
Một máy biến áp có số vòng dây cuộn sơ cấp lớn hơn số vòng dây của cuộn thứ cấp. Máy biến áp này có tác dụng
A. tăng điện áp và cường độ dòng điện.
B. tăng cường độ dòng điện, giảm điện áp.
C. giảm điện áp và cường độ dòng điện.
Hướng dẫn giải:
Cuộn sơ cấp có số vòng là N1, cuộn thứ cấp có số vòng là N2.
Ta có: \(\frac{{{N_1}}}{{{N_2}}} = \frac{{{U_1}}}{{{U_2}}} = \frac{{{I_2}}}{{{I_1}}}\)
\({N_1} > {N_2} \Rightarrow {U_1} > {U_2};{I_1} < {I_2}\)
Chọn B
Câu 4:
Muốn làm giảm hao phí do tỏa nhiệt của dòng fuco gây trên khối kim loại người ta thường
Muốn làm giảm hao phí do tỏa nhiệt của dòng fuco gây trên khối kim loại người ta thường
A. đúc khối kim loại không có phần rỗng bên trong.
B. chia khối kim loại thành nhiều lá kim loại mỏng ghép cách điện nhau.
C. sơn phủ lên khối kim loại một lớp sơn cách điện.
Hướng dẫn giải:
Muốn làm giảm hao phí do tỏa nhiệt của dòng fuco gây trên khối kim loại người ta thường chia khối kim loại thành nhiều lá kim loại mỏng ghép cách điện nhau. Khi đó dòng fuco chỉ chạy trong từng lá mỏng, vì từng lá đơn lẻ có kích thước nhỏ nên có điện trở lớn, cường độ dòng điện fuco trong các lá sẽ giảm đi nhiều so với cường độ dòng điện fuco trong cả khối lớn.
Chọn B
Câu 5:
Bằng đường dây truyền tải một pha, điện năng từ một nhà máy phát điện nhỏ được đưa đến một khu tái định cư. Các kĩ sư tính toán được rằng: nếu tăng điện áp truyền đi từ U lên 2U thì số hộ dân được nhà máy cung cấp đủ điện năng tăng từ 36 lên 144. Biết rằng chỉ có hao phí trên đường dây là đáng kể; các hộ dân tiêu thụ điện năng như nhau. Điện áp truyền đi là 3U, nhà máy này cung cấp đủ điện năng cho bao nhiêu hộ dân?
Trả lời: _______ hộ dân.
Bằng đường dây truyền tải một pha, điện năng từ một nhà máy phát điện nhỏ được đưa đến một khu tái định cư. Các kĩ sư tính toán được rằng: nếu tăng điện áp truyền đi từ U lên 2U thì số hộ dân được nhà máy cung cấp đủ điện năng tăng từ 36 lên 144. Biết rằng chỉ có hao phí trên đường dây là đáng kể; các hộ dân tiêu thụ điện năng như nhau. Điện áp truyền đi là 3U, nhà máy này cung cấp đủ điện năng cho bao nhiêu hộ dân?
Trả lời: _______ hộ dân.
Đáp án đúng: “164”
Hướng dẫn giải:
Công suất điện của nhà máy: P
Công suất tiêu thụ của mỗi hộ dân là P0
Điện trở đường dây tải là R
n là số hộ dân được cung cấp điện khi điện áp truyền đi là 3U
Công suất hao phí trên đường dây: \(\Delta P = \frac{{{P^2}R}}{{{U^2}}}\)
Theo bài ta có:
\(P = 36{P_0} + \frac{{{P^2}R}}{{{U^2}}}\) (1)
\(P = 144{P_0} + \frac{{{P^2}R}}{{4{U^2}}}\) (2)
\(P = n{P_0} + \frac{{{P^2}R}}{{9{U^2}}}\) (3)
Giải các phương trình trên ta tìm được n = 164
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
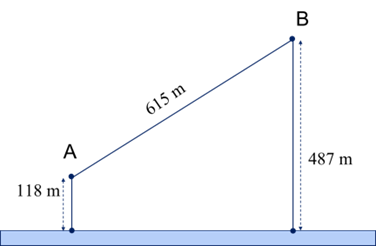
A. 741,2 m.
Lời giải
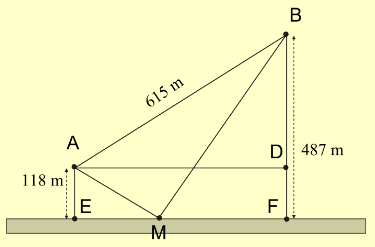
Giả sử người đó đi từ A đến M để lấy nước và đi từ M về B. Dễ dàng tính được BD = 369, EF = 492. Ta đặt EM = x, khi đó:
\(MF = 492 - x,AM = \sqrt {{x^2} + {{118}^2}} ,BM = \sqrt {{{(492 - x)}^2} + {{487}^2}} .\)
Như vậy ta có hàm số f(x) được xác định bằng tổng quãng đường AM và MB :
\(f(x) = \sqrt {{x^2} + {{118}^2}} + \sqrt {{{(492 - x)}^2} + {{487}^2}} \) với \(x \in [0;492]\)
Ta cần tìm giá trị nhỏ nhất của f(x) để có quãng đường ngắn nhất và từ đó xác định được vị trí điểm M.
\(f'(x) = \frac{x}{{\sqrt {{x^2} + {{118}^2}} }} - \frac{{492 - x}}{{\sqrt {{{(492 - x)}^2} + {{487}^2}} }}\)
\(f'(x) = 0 \Leftrightarrow \frac{x}{{\sqrt {{x^2} + {{118}^2}} }} - \frac{{492 - x}}{{\sqrt {{{(492 - x)}^2} + {{487}^2}} }} = 0\)
\( \Leftrightarrow \frac{x}{{\sqrt {{x^2} + {{118}^2}} }} = \frac{{492 - x}}{{\sqrt {{{(492 - x)}^2} + {{487}^2}} }}\)
\( \Leftrightarrow x\sqrt {{{(492 - x)}^2} + {{487}^2}} = (492 - x)\sqrt {{x^2} + {{118}^2}} \)
\( \Leftrightarrow \left\{ \begin{array}{l}{x^2}\left[ {{{(492 - x)}^2} + {{487}^2}} \right] = {\left( {492 - x} \right)^2}\left( {{x^2} + {{118}^2}} \right)\\0 \le x \le 492\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}{(487x)^2} = {(58056 - 118x)^2}\\0 \le x \le 492\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}x = \frac{{58056}}{{605}}{\rm{ hay }}x = - \frac{{58056}}{{369}}\\0 \le x \le 492\end{array} \right.\)
\( \Leftrightarrow x = \frac{{58056}}{{605}}\)
Hàm số \(f(x)\) liên tục trên đoạn [0; 492]. So sánh các giá trị của \(f(0),f\left( {\frac{{58056}}{{605}}} \right),f(492)\) ta có giá trị nhỏ nhất là \(f\left( {\frac{{58056}}{{605}}} \right) \approx 779,8\;{\rm{m}}\).
Chọn B
Câu 2
Lời giải
Chọn đáp án C
Câu 3
A. \({\rm{C}}{{\rm{H}}_3}{\rm{COOH}} + {\rm{CH}} \equiv {\rm{CH}} \to {\rm{C}}{{\rm{H}}_3}{\rm{COOCH}} = {\rm{C}}{{\rm{H}}_2}\).
B. \({\rm{C}}{{\rm{H}}_2} = {\rm{CHCOOH}} + {\rm{C}}{{\rm{H}}_3}{\rm{OH}} \to {\rm{C}}{{\rm{H}}_2} = \) \({\rm{CHCOOC}}{{\rm{H}}_3} + {{\rm{H}}_2}{\rm{O}}\).
C. \({\rm{C}}{{\rm{H}}_3}{\rm{COOH}} + {\rm{C}}{{\rm{H}}_2} = {\rm{CHOH}} \to {\rm{C}}{{\rm{H}}_3}{\rm{COOCH}} = \) \({\rm{C}}{{\rm{H}}_2} + {{\rm{H}}_2}{\rm{O}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.