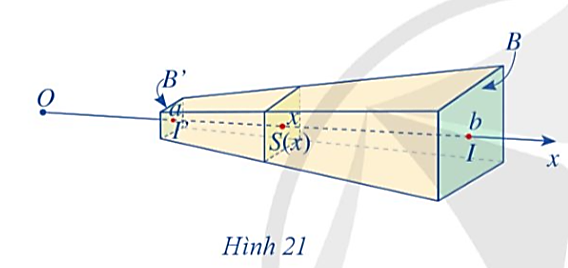
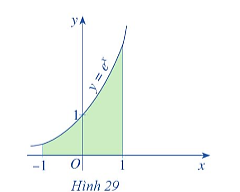
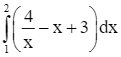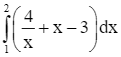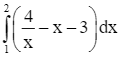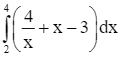Cho tam giác vuông OPM có cạnh OP nằm trên trục Ox. Giả sử 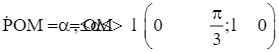 .
.
Gọi 𝒩 là khối tròn xoay thu được khi quay tam giác đó xung quanh trục Ox (Hình 35). Tính thể tích của 𝒩 theo α và ℓ.
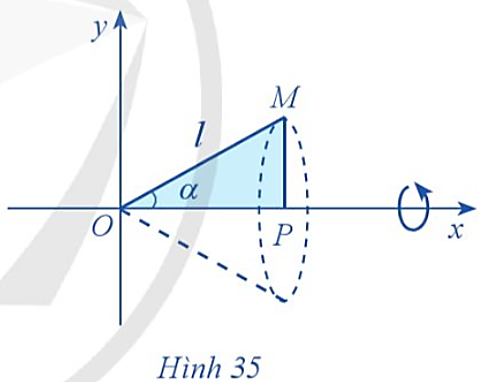
Cho tam giác vuông OPM có cạnh OP nằm trên trục Ox. Giả sử 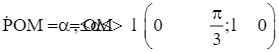 .
.
Gọi 𝒩 là khối tròn xoay thu được khi quay tam giác đó xung quanh trục Ox (Hình 35). Tính thể tích của 𝒩 theo α và ℓ.

Quảng cáo
Trả lời:
Cách 1:
Tam giác OMP là tam giác vuông tại P nên:
OP = OM ∙ ![]() = ℓ ∙ cos α;
= ℓ ∙ cos α;
MP = OM ∙ ![]() = ℓ ∙ sin α;
= ℓ ∙ sin α;
Khi đó, điểm M có tọa độ là 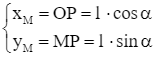 . Suy ra
. Suy ra 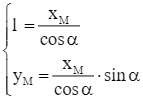 .
.
Suy ra yM = xM ∙ tan α. Do đó điểm M thuộc đường thẳng y = x ∙ tan α.
Lại có điểm O cũng thuộc đường thẳng trên nên phương trình đường thẳng OM là:
y = x ∙ tan α.
Khi đó, tam giác OPM là hình phẳng giới hạn bởi đồ thị hàm số y = x ∙ tan α, trục Ox và hai đường thẳng x = 0, x = ℓ ∙ cos α. Khối tròn xoay 𝒩 là khối tròn xoay thu được khi quay hình phẳng trên quanh trục Ox.
Thể tích khối tròn xoay này là:
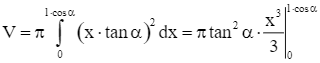
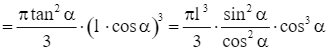
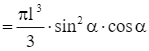 .
.
Cách 2:
Tam giác OMP là tam giác vuông tại P nên:
OP = OM ∙ ![]() = ℓ ∙ cos α;
= ℓ ∙ cos α;
MP = OM ∙ ![]() = ℓ ∙ sin α;
= ℓ ∙ sin α;
Khi quay tam giác OPM quanh trục Ox ta được khối nón tròn xoay có bán kính đáy là r = MP = ℓ ∙ sin α và chiều cao h = OP = ℓ ∙ cos α.
Thể tích khối nón là:
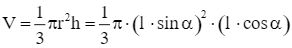
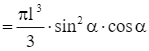 .
.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
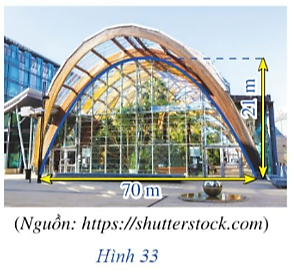
Chọn hệ tọa độ Oxy với gốc tọa độ O trùng với chân cửa bên trái như hình dưới đây.
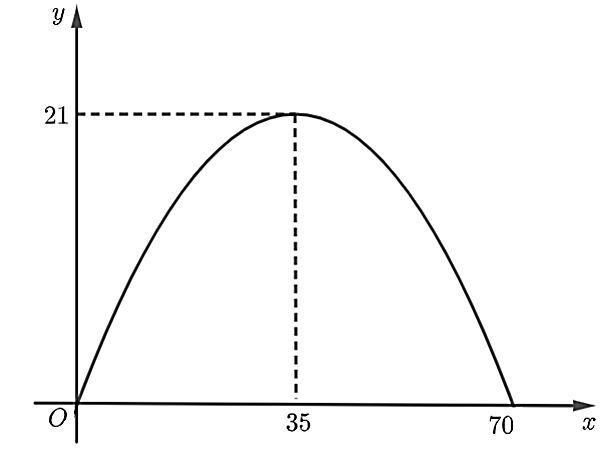
Gọi đồ thị hàm số biểu thị cho cửa đã cho có dạng y = ax2 + bx + c (a ≠ 0).
Đồ thị hàm số này đi qua gốc tọa độ O(0; 0) và các điểm (35; 21), (70; 0) nên
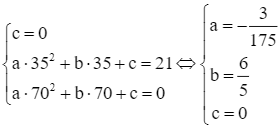 .
.
Suy ra 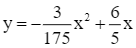 .
.
Diện tích mặt kính cần lắp V là diện tích hình phẳng giới hạn bởi đồ thị hàm số 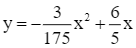 , trục Ox và hai đường thẳng x = 0, x = 70.
, trục Ox và hai đường thẳng x = 0, x = 70.
Ta có 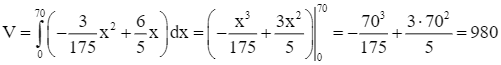 (m2).
(m2).
Lời giải
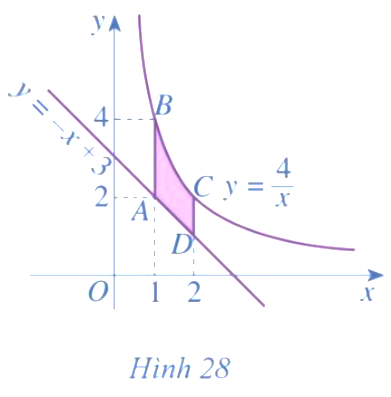
Thể tích của vật thể đã cho là:
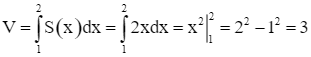 .
.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.