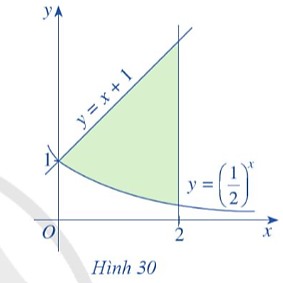
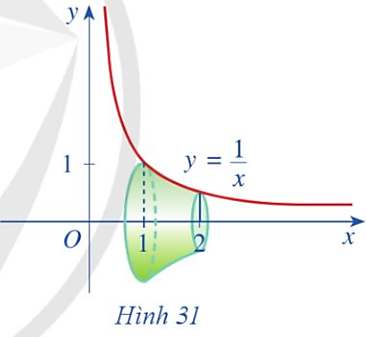
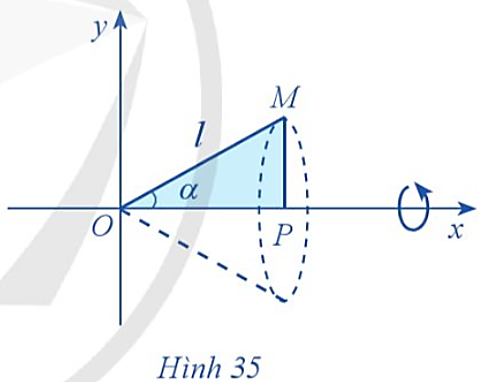
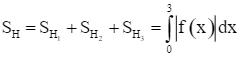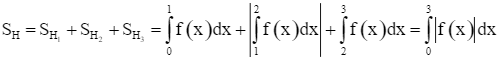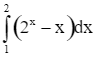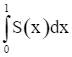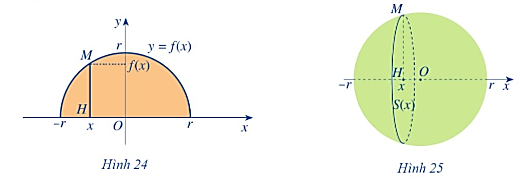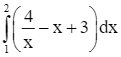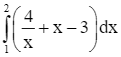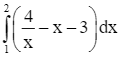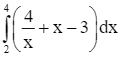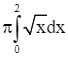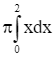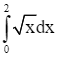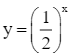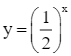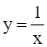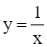Giải SGK Toán 12 CD Bài 4. Ứng dụng hình học của tích phân có đáp án
66 người thi tuần này 4.6 608 lượt thi 29 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 3
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 2
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 1
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 3
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 2
Danh sách câu hỏi:
Lời giải
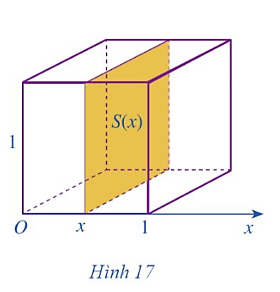
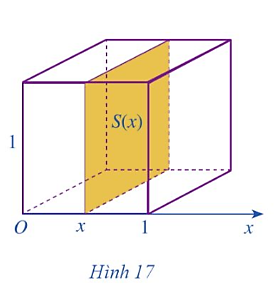
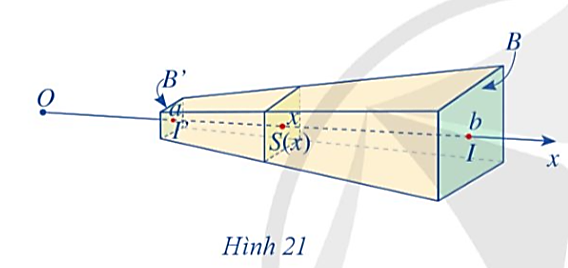
Sau bài học này ta biết được để tính thể tích của các khối tròn xoay, ta cần xác định khối tròn xoay đó được giới hạn bởi các đồ thị hàm số nào, sau đó, sử dụng tích phân để giải quyết.
Lời giải
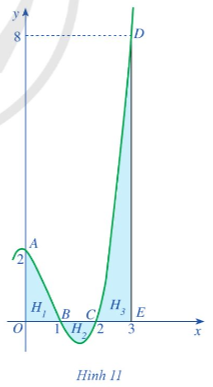
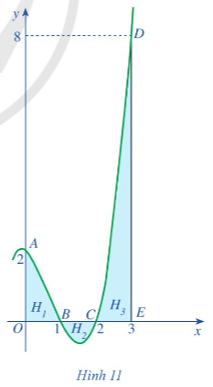
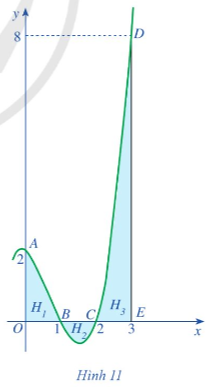
Quan sát Hình 11, ta thấy:
+ Hình phẳng H1 được giới hạn bởi các đường thẳng x = 0, x = 1, trục Ox và đồ thị hàm số y = f(x) = x3 – 2x2 – x + 2.
+ Hình phẳng H2 được giới hạn bởi các đường thẳng x = 1, x = 2, trục Ox và đồ thị hàm số y = f(x) = x3 – 2x2 – x + 2.
+ Hình phẳng H3 được giới hạn bởi các đường thẳng x = 2, x = 3, trục Ox và đồ thị hàm số y = f(x) = x3 – 2x2 – x + 2.
Lời giải
Ta có:
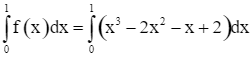
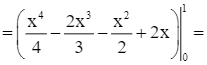
![]() .
.
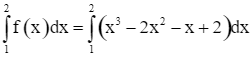
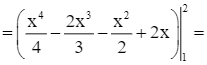
![]() .
.
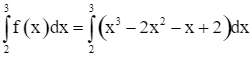
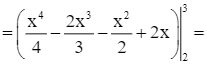
![]() .
.
Do đó, 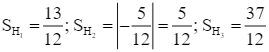 .
.
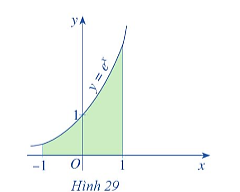
Lời giải
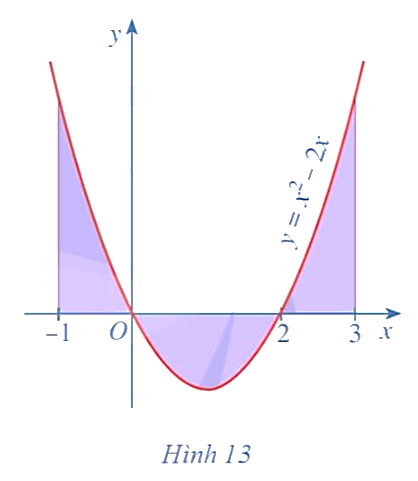
Diện tích hình phẳng giới hạn bởi đồ thị của hàm số y = x2 – 2x, trục Ox và hai đường thẳng x = – 1, x = 3 là:
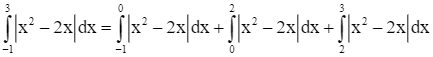
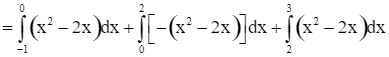
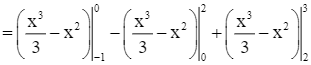
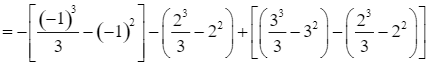
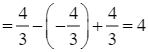 .
.
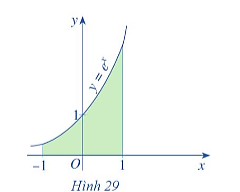
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
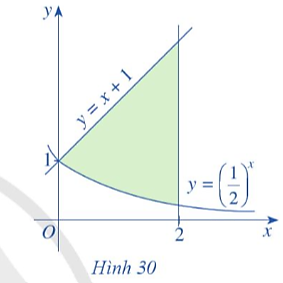
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.