Giải SGK Toán 12 Cánh diều Bài 3. Đường tiệm cận của đồ thị hàm số có đáp án

25 người thi tuần này 4.6 1.1 K lượt thi 13 câu hỏi

Đề số 1

🔥 Học sinh cũng đã học

142 người thi tuần này

Đề thi cuối kì 1 Toán 12 năm 2025-2026 THPT Lê Trọng Tấn (TP.HCM) có đáp án

1.1 K lượt thi 22 câu hỏi

80 người thi tuần này

Đề thi cuối kì 1 Toán 12 năm 2025-2026 THPT Thủ Đức (TP.HCM) có đáp án

1 K lượt thi 22 câu hỏi

79 người thi tuần này

Đề thi cuối kì 1 Toán 12 năm 2025-2026 THPT Ngô Quyền (TP.HCM) có đáp án

1 K lượt thi 22 câu hỏi

76 người thi tuần này

Đề thi cuối kì 1 Toán 12 năm 2025-2026 THPT Mạc Đĩnh Chi (TP.HCM) có đáp án

1 K lượt thi 21 câu hỏi

74 người thi tuần này

Đề thi cuối kì 1 Toán 12 năm 2025-2026 THCS - THPT Trần Cao Vân (TP.HCM) có đáp án

1 K lượt thi 22 câu hỏi

72 người thi tuần này

Đề thi cuối kì 1 Toán 12 năm 2025-2026 THPT Bùi Thị Xuân (TP.HCM) có đáp án

1 K lượt thi 22 câu hỏi

73 người thi tuần này

Đề thi cuối kì 1 Toán 12 năm 2025-2026 THPT Marie Curie (TP.HCM) có đáp án

1 K lượt thi 22 câu hỏi

78 người thi tuần này

Đề thi cuối kì 1 Toán 12 năm 2025-2026 THPT Nguyễn Thị Minh Khai (TP.HCM) có đáp án

1 K lượt thi 22 câu hỏi

Danh sách câu hỏi:

Câu 1/13

Số dân của một thị trấn sau x năm kể từ năm 1970 được ước tính bởi công thức

$y = f (x) = \frac{26 x + 10}{x + 5}$

(f(x) được tính bằng nghìn người) (Nguồn: Giải tích 12 Nâng cao, NXBGD Việt Nam, 2020). Xem y = f(x) là một hàm số xác định trên nửa khoảng [0; + ∞), đồ thị của hàm số đó là đường cong màu xanh ở Hình 10.

Khi x → + ∞, đồ thị hàm số y = f(x) ngày càng “tiến gần” tới đường thẳng nào?

Xem đáp án

Lời giải

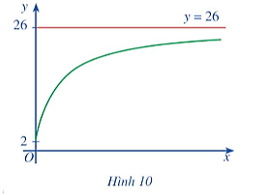
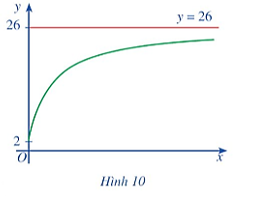
Khi x → + ∞, đồ thị hàm số y = f(x) ngày càng “tiến gần” tới đường thẳng y = 26.

Câu 2/13

Xét hàm số y = f(x) = $\frac{26 x + 10}{x + 5}$ , với x ∈ [0; + ∞) có đồ thị là đường cong ở Hình 10 trong bài toán mở đầu. Tìm $\lim_{x \to + \infty} f (x)$

Xem đáp án

Lời giải

Quan sát đồ thị ở Hình 10, ta thấy x → + ∞ thì y → 26.

Vậy $\lim_{x \to + \infty} f (x) = 26$ .

Câu 3/13

Tìm tiệm cận ngang của đồ thị hàm số $y = \frac{3 x - 2}{x + 1}$

Xem đáp án

Lời giải

Hàm số đã cho có tập xác định là ℝ \ {– 1}.

Ta có: $\lim_{x \to + \infty} y = \lim_{x \to + \infty} \frac{3 x - 2}{x + 1} = 3$ ,

$\lim_{x \to - \infty} y = \lim_{x \to - \infty} \frac{3 x - 2}{x + 1} = 3$ .

Vậy đường thẳng y = 3 là tiệm cận ngang của đồ thị hàm số đã cho.

Câu 4/13

Cho hàm số y = f(x) = $\frac{1}{x}$ có đồ thị là đường cong như Hình 12.

Tìm $\lim_{x \to 0^{+}} f (x), \lim_{x \to 0^{-}} f (x)$ .

Xem đáp án

Lời giải

Quan sát đồ thị ở Hình 12, ta thấy:

+) x → 0⁺ thì f(x) → + ∞, do đó $\lim_{x \to 0^{+}} f (x) = + \infty$ ;

+) x → 0^– thì f(x) → – ∞, do đó $\lim_{x \to 0^{-}} f (x) = - \infty$ .

Câu 5/13

Tìm tiệm cận đứng của đồ thị hàm số $y = \frac{x^{2} + 3 x}{x - 5}$ .

Xem đáp án

Lời giải

Hàm số đã cho có tập xác định là ℝ\{5}.

Ta có $\lim_{x \to 5^{+}} y = \lim_{x \to 5^{+}} \frac{x^{2} + 3 x}{x - 5} = + \infty$ (do $\lim_{x \to 5^{+}} (x^{2} + 3 x) = 40 > 0, \lim_{x \to 5^{+}} (x - 5) = 0$ , khi x → 5⁺ thì x – 5 > 0).

Tương tự $\lim_{x \to 5^{-}} y = \lim_{x \to 5^{-}} \frac{x^{2} + 3 x}{x - 5} = - \infty$ .

Vậy đường thẳng x = 5 là tiệm cận đứng của đồ thị hàm số đã cho.

Câu 6/13

Cho hàm số $y = f (x) = x + 1 + \frac{1}{x - 1}$ có đồ thị là (C) và đường thẳng y = x + 1 (Hình 15).

Tìm $\lim_{x \to + \infty} [f (x) - (x + 1)]; \lim_{x \to - \infty} [f (x) - (x + 1)]$ .

Xem đáp án

Lời giải

Ta có $\lim_{x \to + \infty} [f (x) - (x + 1)] = \lim_{x \to + \infty} \frac{1}{x - 1} = 0$ ;

$\lim_{x \to - \infty} [f (x) - (x + 1)] = \lim_{x \to - \infty} \frac{1}{x - 1} = 0$ .

Câu 7/13

Chứng minh rằng đường thẳng y = – x là tiệm cận xiên của đồ thị hàm số $y = f (x) = \frac{- x^{2} - 2 x + 3}{x + 2}$ .

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 8/13

Tìm tiệm cận xiên của đồ thị hàm số $y = f (x) = \frac{x^{2} - 3 x + 2}{x + 3}$ .

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 9/13

Tiệm cận đứng của đồ thị hàm số $y = \frac{x + 2}{x + 1}$ là:

A. x = – 1.

B. x = – 2.

C. x = 1.

D. x = 2.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 10/13

Tiệm cận xiên của đồ thị hàm số $y = \frac{x^{2} + 3 x + 5}{x + 2}$ là:

A. y = x.

B. y = x + 1.

C. y = x + 2.

D. y = x + 3.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 11/13

Đồ thị hàm số ở Hình 18a, Hình 18b đều có đường tiệm cận ngang là đường thẳng màu đỏ. Hỏi đó là đồ thị của hàm số nào trong các hàm số sau?

a) $y = \frac{x^{2} + 2 x - 1}{x^{2} + 1}$ ;

b) $y = \frac{2 x^{2} + x + 1}{x - 1}$ ;

c) $y = \frac{2 x^{2} - 2}{x^{2} + 2}$ .

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 12/13

Số lượng sản phẩm bán được của một công ty trong x (tháng) được tính theo công thức $S (x) = 200 (5 - \frac{9}{2 + x})$ , trong đó x ≥ 1 (Nguồn: R. Larson and B. Edwards, Calculus 10e, Cengage 2014).

a) Xem y = S(x) là một hàm số xác định trên nửa khoảng [1; + ∞), hãy tìm tiệm cận ngang của đồ thị hàm số đó.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 13/13

b) Nêu nhận xét về số lượng sản phẩm bán được của công ty đó trong x (tháng) khi x đủ lớn.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem tiếp với tài khoản VIP

Còn 7/13 câu hỏi, đáp án và lời giải chi tiết.

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Lớp 12

Lớp 11

Lớp 10

Ôn vào 10

Lớp 9

Lớp 8

Lớp 7

Lớp 6

Ôn vào 6

Lớp 5

Lớp 4

Lớp 3

Lớp 2

Lớp 1

Đại học

ĐGNL - ĐGTD

Tốt nghiệp THPT

Ôn vào 10

Ôn vào 6

V-ACT

HSA

TSA

SPT

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Hóa học

Lịch sử

Địa lí

Toán

Văn

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Khoa học tự nhiên

Tin học

Lịch sử

Địa lí

Toán

Văn

Tiếng Anh

Khoa học tự nhiên

Lịch sử & Địa lí

Giáo dục công dân

Tin học

Công nghệ

Toán

Tiếng Anh

Khoa học tự nhiên

Lịch sử & Địa lí

Giáo dục công dân

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Khoa học tự nhiên

Lịch sử & Địa lí

Giáo dục công dân

Tin học

Xét hàm số y = f(x) = $\frac{26 x + 10}{x + 5}$ , với x ∈ [0; + ∞) có đồ thị là đường cong ở Hình 10 trong bài toán mở đầu. Tìm $\lim_{x \to + \infty} f (x)$

Tìm tiệm cận ngang của đồ thị hàm số $y = \frac{3 x - 2}{x + 1}$

Cho hàm số y = f(x) = $\frac{1}{x}$ có đồ thị là đường cong như Hình 12.

Tìm $\lim_{x \to 0^{+}} f (x), \lim_{x \to 0^{-}} f (x)$ .

Tìm tiệm cận đứng của đồ thị hàm số $y = \frac{x^{2} + 3 x}{x - 5}$ .

Cho hàm số $y = f (x) = x + 1 + \frac{1}{x - 1}$ có đồ thị là (C) và đường thẳng y = x + 1 (Hình 15).

Tìm $\lim_{x \to + \infty} [f (x) - (x + 1)]; \lim_{x \to - \infty} [f (x) - (x + 1)]$ .

Chứng minh rằng đường thẳng y = – x là tiệm cận xiên của đồ thị hàm số $y = f (x) = \frac{- x^{2} - 2 x + 3}{x + 2}$ .

Tìm tiệm cận xiên của đồ thị hàm số $y = f (x) = \frac{x^{2} - 3 x + 2}{x + 3}$ .

Tiệm cận đứng của đồ thị hàm số $y = \frac{x + 2}{x + 1}$ là:

A. x = – 1.

B. x = – 2.

C. x = 1.

D. x = 2.

Tiệm cận xiên của đồ thị hàm số $y = \frac{x^{2} + 3 x + 5}{x + 2}$ là:

A. y = x.

B. y = x + 1.

C. y = x + 2.

D. y = x + 3.