1. Lớp 12
  2. Toán
  3. Giải SGK Toán 12 CD Bài 2. Phương trình đường thẳng có đáp án

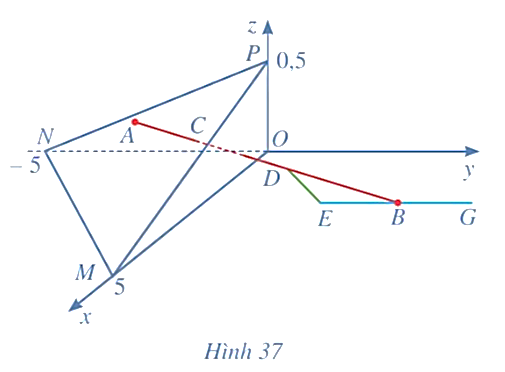
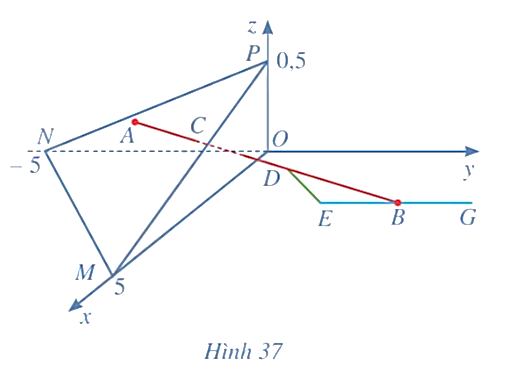
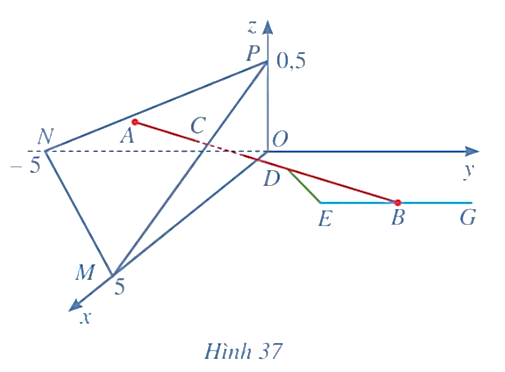
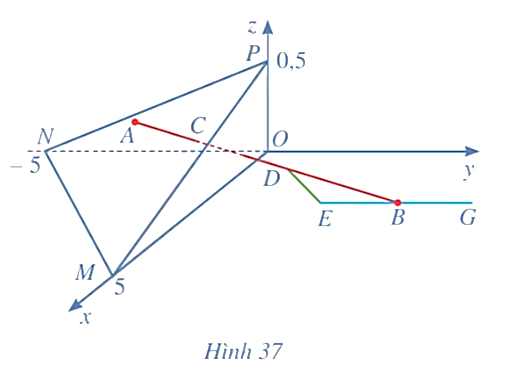
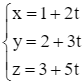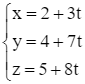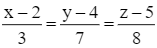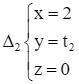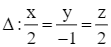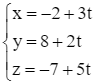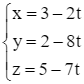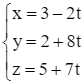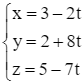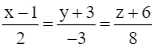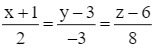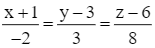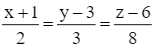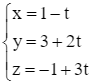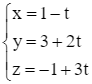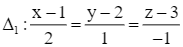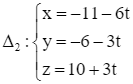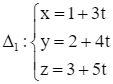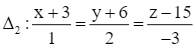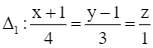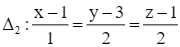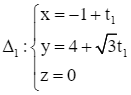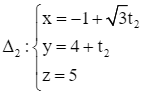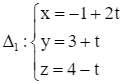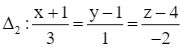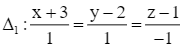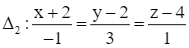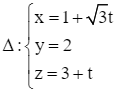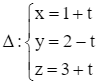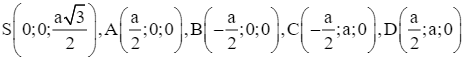Giải SGK Toán 12 CD Bài 2. Phương trình đường thẳng có đáp án

55 người thi tuần này 4.6 369 lượt thi 54 câu hỏi

🔥 Đề thi HOT:

1575 người thi tuần này

7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án ( Phần 1)

71.2 K lượt thi 304 câu hỏi
909 người thi tuần này

20 câu Trắc nghiệm Phương trình đường thẳng trong không gian có đáp án (Nhận biết)

11.5 K lượt thi 20 câu hỏi
826 người thi tuần này

5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)

68.2 K lượt thi 126 câu hỏi
720 người thi tuần này

237 câu Bài tập Hàm số mũ, logarit ôn thi Đại học có lời giải (P1)

22.2 K lượt thi 30 câu hỏi
707 người thi tuần này

124 câu Trắc nghiệm Ôn tập Toán 12 Chương 3 Hình học có đáp án (Phần 1)

13.2 K lượt thi 25 câu hỏi
666 người thi tuần này

79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án

12 K lượt thi 40 câu hỏi
629 người thi tuần này

15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)

10.9 K lượt thi 15 câu hỏi
626 người thi tuần này

7 câu Trắc nghiệm Khối đa diện lồi và khối đa diện đều có đáp án (Vận dụng)

10.2 K lượt thi 7 câu hỏi

Nội dung liên quan:

Giải SGK Toán 12 CD Bài 1. Phương trình mặt phẳng có đáp án
lượt thi
1 đề

Giải SGK Toán 12 CD Bài 3. Phương trình mặt cầu có đáp án
lượt thi
1 đề

Giải SGK Toán 12 CD Bài tập cuối chương 5 có đáp án
lượt thi
1 đề

Danh sách câu hỏi:

Câu 1

Cầu Bãi Cháy nối Hòn Gai và Bãi Cháy (Quảng Ninh). Dây cáp của cầu gợi nên hình ảnh đường thẳng trong không gian với hệ tọa độ Oxyz (Hình 22).

Trong hệ tọa độ Oxyz, phương trình của đường thẳng là gì? Làm thế nào để lập được phương trình của đường thẳng?

Lời giải

Trong bài học này, ta sẽ tìm hiểu phương trình của đường thẳng trong hệ tọa độ Oxyz và cách lập phương trình của đường thẳng.

Câu 2

Cho hình hộp ABCD.A'B'C'D' (Hình 23). Giá của vectơ và đường thẳng AC có vị trí tương đối như thế nào?

Lời giải

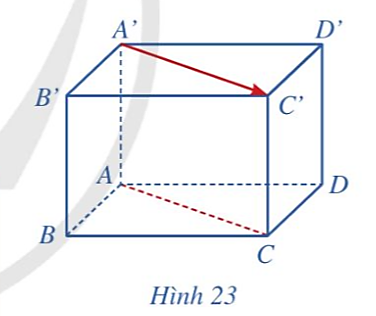
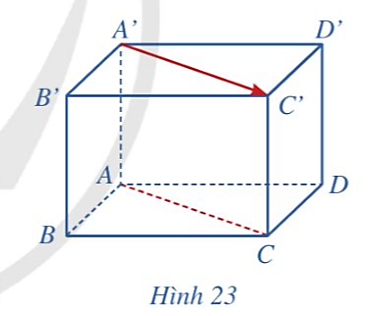
Giá của vectơ là đường thẳng A'C'.

Vì ABCD.A'B'C'D' là hình hộp nên AC // A'C'.

Vậy giá của vectơ và đường thẳng AC song song với nhau.

Câu 3

Trong Hình 23, vectơ có là vectơ chỉ phương của đường thẳng BD hay không? Vì sao?

Lời giải

Do vectơ khác và có giá là đường thẳng B'D' song song với đường thẳng BD nên vectơ là vectơ chỉ phương của đường thẳng BD.

Câu 4

Trong không gian với hệ tọa độ Oxyz, cho đường thẳng ∆ đi qua điểm M0(1; 2; 3) và có vectơ chỉ phương . Xét điểm M(x; y; z) nằm trên ∆ (Hình 24).

Nêu nhận xét về phương của hai vectơ và .

Lời giải

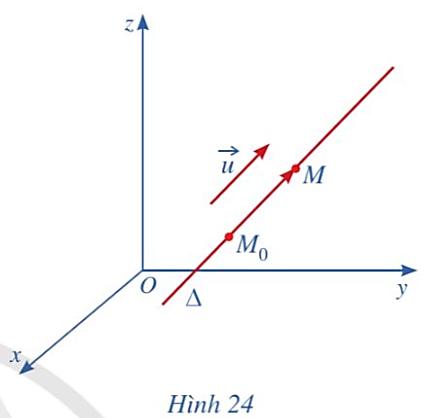
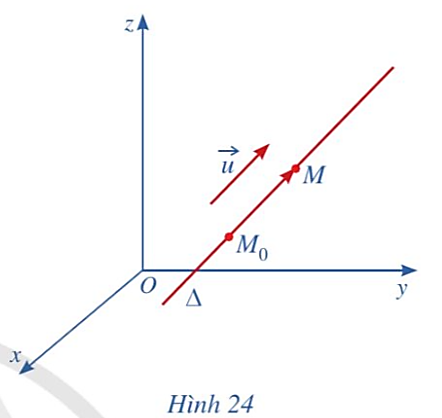
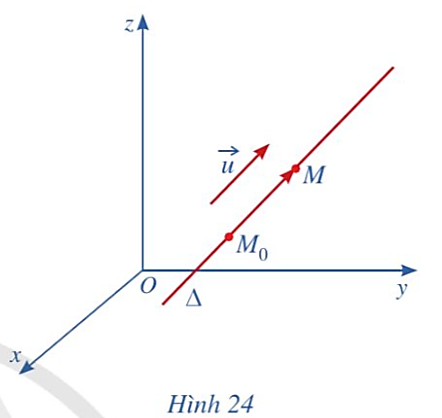
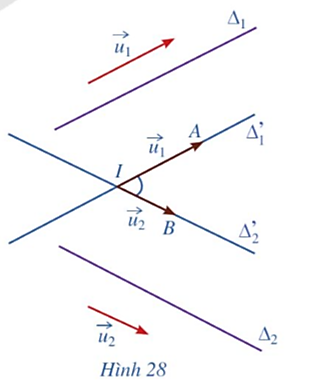
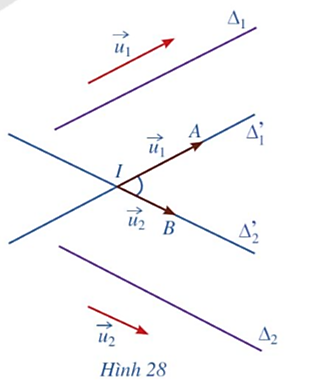
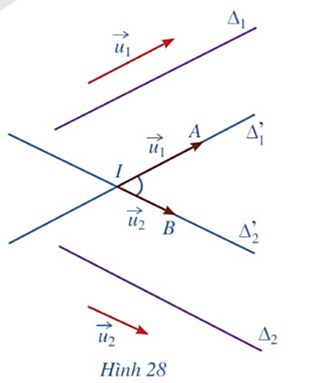
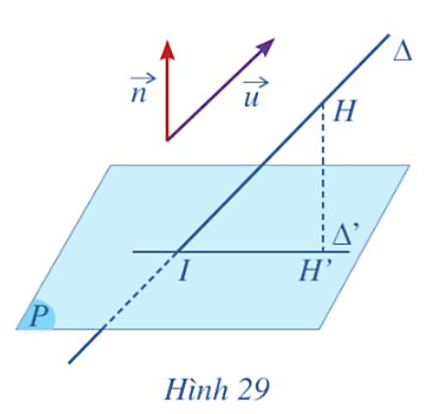
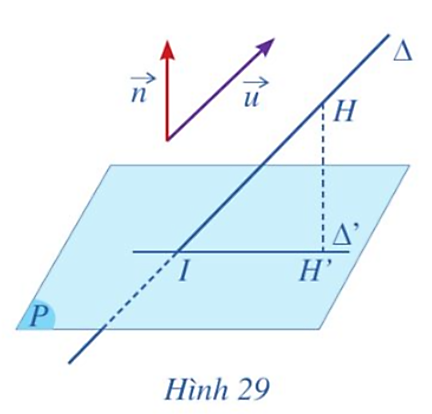
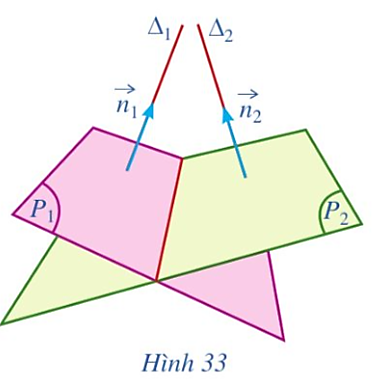
Vì vectơ là vectơ chỉ phương của đường thẳng ∆ nên giá của vectơ song song hoặc trùng với đường thẳng ∆.

Lại có vectơ có giá là đường thẳng M0M hay chính là đường thẳng ∆.

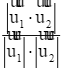
Từ đó suy ra hai vectơ và có giá song song hoặc trùng nhau nên chúng cùng phương.

Câu 5

Trong không gian với hệ tọa độ Oxyz, cho đường thẳng ∆ đi qua điểm M0(1; 2; 3) và có vectơ chỉ phương . Xét điểm M(x; y; z) nằm trên ∆ (Hình 24).

Có hay không số thực t sao cho ?

Lời giải

Vì hai vectơ và cùng phương nên tồn tại số thực t ≠ 0 sao cho .

Câu 6

Trong không gian với hệ tọa độ Oxyz, cho đường thẳng ∆ đi qua điểm M0(1; 2; 3) và có vectơ chỉ phương . Xét điểm M(x; y; z) nằm trên ∆ (Hình 24).

Hãy biểu diễn x, y, z qua t.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

 Trong không gian với hệ tọa độ Oxyz, cho đường thẳng ∆ đi qua điểm M0(1; 2; 3) và có vectơ chỉ phương . Xét điểm M(x; y; z) nằm trên ∆ (Hình 24).

Tọa độ (x; y; z) của điểm M (nằm trên ∆) có thỏa mãn hệ phương trình:

hay không?

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 8

Viết phương trình tham số của đường thẳng ∆, biết ∆ đi qua điểm C(1; 2; – 4) và vuông góc với mặt phẳng (P):

3x – y + 2z – 1 = 0.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 9

Cho đường thẳng ∆ có phương trình tham số:

(t là tham số).

Tọa độ (x; y; z) của điểm M (nằm trên ∆) có thỏa mãn hệ phương trình

hay không?

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 10

Viết phương trình chính tắc của đường thẳng ∆, biết phương trình tham số của ∆ là: (t là tham số).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 11

Trong không gian với hệ tọa độ Oxyz, cho điểm A(1; 2; 3) và B(3; 5; 9).
Hãy chỉ ra một vectơ chỉ phương của đường thẳng AB.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 12

Trong không gian với hệ tọa độ Oxyz, cho điểm A(1; 2; 3) và B(3; 5; 9).
Viết phương trình tham số của đường thẳng AB.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 13

Trong không gian với hệ tọa độ Oxyz, cho điểm A(1; 2; 3) và B(3; 5; 9).
Viết phương trình chính tắc của đường thẳng AB.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 14

Viết phương trình chính tắc của đường thẳng OM, biết M(a; b; c) với abc ≠ 0.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 15

Cho hai đường thẳng phân biệt ∆1, ∆2 lần lượt đi qua các điểm M1, M2 và tương ứng có vectơ chỉ phương là .

Giả sử ∆1 song song với ∆2 (Hình 25). Các cặp vectơ sau có cùng phương hay không: và ; và ?

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 16

Cho hai đường thẳng phân biệt ∆1, ∆2 lần lượt đi qua các điểm M1, M2 và tương ứng có vectơ chỉ phương là .

Giả sử ∆1 và ∆2 cắt nhau (Hình 26). Hai vectơ và có cùng phương hay không? Ba vectơ , và có đồng phẳng hay không?

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 17

Cho hai đường thẳng phân biệt ∆1, ∆2 lần lượt đi qua các điểm M1, M2 và tương ứng có vectơ chỉ phương là .

Giả sử ∆1 và ∆2 chéo nhau (Hình 27). Hai vectơ và có cùng phương hay không? Ba vectơ , và có đồng phẳng hay không?

 

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 18

Bằng cách giải hệ phương trình, xác định vị trí tương đối của hai đường thẳng và (t1, t2 là tham số).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 19

Cho hai đường thẳng ∆1, ∆2 trong không gian có vectơ chỉ phương lần lượt là . Giả sử ∆'1, ∆'2 là hai đường thẳng cùng đi qua điểm I và lần lượt song song (hoặc trùng) với ∆1, ∆2 (Hình 28).

Nếu mối liên hệ giữa hai góc (∆1, ∆2) và (∆'1, ∆'2).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 20

Cho hai đường thẳng ∆1, ∆2 trong không gian có vectơ chỉ phương lần lượt là . Giả sử ∆'1, ∆'2 là hai đường thẳng cùng đi qua điểm I và lần lượt song song (hoặc trùng) với ∆1, ∆2 (Hình 28).

Gọi A và B là các điểm lần lượt thuộc hai đường thẳng ∆'1 và ∆'2 sao cho , . So sánh:

.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 21

Cho hai đường thẳng ∆1, ∆2 trong không gian có vectơ chỉ phương lần lượt là . Giả sử ∆'1, ∆'2 là hai đường thẳng cùng đi qua điểm I và lần lượt song song (hoặc trùng) với ∆1, ∆2 (Hình 28).

So sánh cos (∆1, ∆2) và .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 22

Cho đường thẳng . Tính côsin của góc giữa đường thẳng ∆ và các trục tọa độ.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 23

Cho mặt phẳng (P) có vectơ pháp tuyến là , đường thẳng ∆ có vectơ chỉ phương là và đường thẳng ∆ cắt mặt phẳng (P) tại I. Gọi ∆' là hình chiếu của ∆ trên mặt phẳng (P) (Hình 29).

Hãy xác định góc giữa đường thẳng ∆ và mặt phẳng (P).

Ta kí hiệu góc đó là (∆, (P)).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 24

Cho mặt phẳng (P) có vectơ pháp tuyến là , đường thẳng ∆ có vectơ chỉ phương là và đường thẳng ∆ cắt mặt phẳng (P) tại I. Gọi ∆' là hình chiếu của ∆ trên mặt phẳng (P) (Hình 29).

So sánh sin (∆, (P)) và .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 25

Cho mặt phẳng (P) có vectơ pháp tuyến . Tính sin của góc giữa mặt phẳng (P) và các trục tọa độ.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 26

Cho hai mặt phẳng (P1) và (P2). Lấy hai đường thẳng ∆1, ∆2 sao cho ∆1 ⊥ (P1), ∆2 ⊥ (P2) (Hình 31).

Nêu cách xác định góc giữa hai đường thẳng ∆1, ∆2.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 27

Cho hai mặt phẳng (P1) và (P2). Lấy hai đường thẳng ∆1, ∆2 sao cho ∆1 ⊥ (P1), ∆2 ⊥ (P2) (Hình 31).

Góc đó có phụ thuộc vào việc chọn hai đường thẳng ∆1, ∆2 như trên hay không?

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 28

Trong Ví dụ 10, tính góc giữa hai mặt phẳng (BCC'B') và (CDA'B').

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 29

Cho hai mặt phẳng (P1) và (P2). Gọi lần lượt là hai vectơ pháp tuyến của (P1), (P2); ∆1, ∆2 lần lượt là giá của hai vectơ (Hình 33). So sánh:

cos ((P1), (P2)) và cos (∆1, ∆2);

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 30

Cho hai mặt phẳng (P1) và (P2). Gọi lần lượt là hai vectơ pháp tuyến của (P1), (P2); ∆1, ∆2 lần lượt là giá của hai vectơ (Hình 33). So sánh:

cos (∆1, ∆2) và .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 31

Cho mặt phẳng (P) có vectơ pháp tuyến . Tính côsin của góc giữa mặt phẳng (P) và các mặt phẳng tọa độ.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 32

Đường thẳng đi qua điểm A(3; 2; 5) nhận làm vectơ chỉ phương có phương trình tham số là:

A. .

B. .

C. .

D. .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 33

Đường thẳng đi qua điểm B(– 1; 3; 6) nhận làm vectơ chỉ phương có phương trình chính tắc là:

A. .

B. .

C. .

D. . 

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 34

Mặt phẳng (P): x – 2 = 0 vuông góc với mặt phẳng nào sau đây?

A. (P1): x + 2 = 0.

B. (P2): x + y – 2 = 0.

C. (P3): z – 2 = 0.

D. (P4): x + z – 2 = 0.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 35

Cho đường thẳng ∆ có phương trình tham số (t là tham số).

Chỉ ra tọa độ hai điểm thuộc đường thẳng ∆.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 36

Cho đường thẳng ∆ có phương trình tham số (t là tham số).
Điểm nào trong hai điểm C(6; – 7; – 16), D(– 3; 11; – 11) thuộc đường thẳng ∆?

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 37

Viết phương trình tham số và phương trình chính tắc của đường thẳng ∆ trong mỗi trường hợp sau:

∆ đi qua điểm A(– 1; 3; 2) và có vectơ chỉ phương ;

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 38

Viết phương trình tham số và phương trình chính tắc của đường thẳng ∆ trong mỗi trường hợp sau:
∆ đi qua điểm M(2; – 1; 3) và N(3; 0; 4).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 39

Xác định vị trí tương đối của hai đường thẳng ∆1, ∆2 trong mỗi trường hợp sau:

và (t là tham số);

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 40

Xác định vị trí tương đối của hai đường thẳng ∆1, ∆2 trong mỗi trường hợp sau:
(t là tham số) và ;

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 41

Xác định vị trí tương đối của hai đường thẳng ∆1, ∆2 trong mỗi trường hợp sau:

và .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 42

Tính góc giữa hai đường thẳng ∆1, ∆2 trong mỗi trường hợp sau (làm tròn kết quả đến hàng đơn vị của độ):

và (t1, t2 là tham số);

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 43

Tính góc giữa hai đường thẳng ∆1, ∆2 trong mỗi trường hợp sau (làm tròn kết quả đến hàng đơn vị của độ):
(t là tham số) và ;

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 44

Tính góc giữa hai đường thẳng ∆1, ∆2 trong mỗi trường hợp sau (làm tròn kết quả đến hàng đơn vị của độ):

và .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 45

Tính góc giữa đường thẳng ∆ và mặt phẳng (P) trong mỗi trường hợp sau (làm tròn kết quả đến hàng đơn vị của độ):

(t là tham số) và (P): x + z – 2 = 0;

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 46

Tính góc giữa đường thẳng ∆ và mặt phẳng (P) trong mỗi trường hợp sau (làm tròn kết quả đến hàng đơn vị của độ):
(t là tham số) và (P): x + y + z – 4 = 0.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 47

Tính góc giữa hai mặt phẳng

(P1): x + y + 2z – 1 = 0 và (P2): 2x – y + z – 2 = 0.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 48

Trong không gian với hệ trục tọa độ Oxyz, cho hình chóp S.ABCD có các đỉnh lần lượt là

với a > 0 (Hình 36).

Xác định tọa độ của các vectơ  . Từ đó tính góc giữa hai đường thẳng SA và CD (làm tròn kết quả đến hàng đơn vị của độ).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 49

Trong không gian với hệ trục tọa độ Oxyz, cho hình chóp S.ABCD có các đỉnh lần lượt là

với a > 0 (Hình 36).

Chỉ ra một vectơ pháp tuyến của mặt phẳng (SAC). Từ đó tính góc giữa đường thẳng SD và mặt phẳng (SAC) (làm tròn kết quả đến hàng đơn vị của độ).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 50

Trong không gian với hệ tọa độ Oxyz (đơn vị trên mỗi trục tọa độ là kilômét), một máy bay đang ở vị trí A(3,5; – 2; 0,4) và sẽ hạ cánh ở vị trí B(3,5; 5,5; 0) trên đường băng EG (Hình 37).

Viết phương trình đường thẳng AB.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 51

Trong không gian với hệ tọa độ Oxyz (đơn vị trên mỗi trục tọa độ là kilômét), một máy bay đang ở vị trí A(3,5; – 2; 0,4) và sẽ hạ cánh ở vị trí B(3,5; 5,5; 0) trên đường băng EG (Hình 37).

Hãy cho biết góc trượt (góc giữa đường bay AB và mặt phẳng nằm ngang (Oxy)) có nằm trong phạm vi cho phép từ 2,5° đến 3,5° hay không.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 52

Trong không gian với hệ tọa độ Oxyz (đơn vị trên mỗi trục tọa độ là kilômét), một máy bay đang ở vị trí A(3,5; – 2; 0,4) và sẽ hạ cánh ở vị trí B(3,5; 5,5; 0) trên đường băng EG (Hình 37).

Có một lớp mây được mô phỏng bởi một mặt phẳng (α) đi qua ba điểm M(5; 0; 0), N(0; – 5; 0), P(0; 0; 0,5). Tìm tọa độ của điểm C là vị trí mà máy bay xuyên qua đám mây để hạ cánh.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 53

Trong không gian với hệ tọa độ Oxyz (đơn vị trên mỗi trục tọa độ là kilômét), một máy bay đang ở vị trí A(3,5; – 2; 0,4) và sẽ hạ cánh ở vị trí B(3,5; 5,5; 0) trên đường băng EG (Hình 37).

Tìm tọa độ của điểm D trên đoạn thẳng AB là vị trí mà máy bay ở độ cao 120 m.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 54

Trong không gian với hệ tọa độ Oxyz (đơn vị trên mỗi trục tọa độ là kilômét), một máy bay đang ở vị trí A(3,5; – 2; 0,4) và sẽ hạ cánh ở vị trí B(3,5; 5,5; 0) trên đường băng EG (Hình 37).

Theo quy định an toàn bay, người phi công phải nhìn thấy điểm đầu E(3,5; 4,5; 0) của đường băng ở độ cao tối thiểu là 120 m. Hỏi sau khi ra khỏi đám mây, người phi công có đạt được quy định an toàn đó hay không? Biết rằng tầm nhìn của người phi công sau khi ra khỏi đám mây là 900 m (Nguồn: R.Larson and B.Edwards, Calculus 10e, Cengage, 2014).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
Giấy chứng nhận ĐKKD số: 0108307822 do Sở KH & ĐT TP Hà Nội cấp lần đầu ngày 04/06/2018
© 2017 Vietjack72. All Rights Reserved.
zalo Nhắn tin Zalo

Đăng ký

Bạn đã có tài khoản?