Giải SBT Toán 12 CD Bài 2. Tọa độ của vectơ có đáp án
31 người thi tuần này 4.6 378 lượt thi 8 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Bài tập GTLN, GTNN của hàm số lớp 12 (có lời giải)
Bài tập Một số bài toán thực tế liên quan đến GTLN, GTNN của hàm số lớp 12 (có lời giải)
Bài tập Tìm GTLN – GTNN của hàm số y = f(x) trên đoạn lớp 12 (có lời giải)
Bài tập Tìm GTLN – GTNN của hàm số y = f(x) trên khoảng, nửa khoảng lớp 12 (có lời giải)
Bài tập Tìm GTLN – GTNN bằng hình ảnh đồ thị cho trước lớp 12 (có lời giải)
Danh sách câu hỏi:
Lời giải
Đáp án đúng là: A
Ta có: O(0; 0; 0), A(−1; 5; 3) nên 
= (−1; 5; 3).
Lời giải
Đáp án đúng là: B
Ta có: 
= 
nên = (1; −2; 4), suy ra A(1; −2; 4).
Lời giải
Đáp án đúng là: D
Ta có: 
⇒ 
= (−3; 1; −5).
Lời giải
Đáp án đúng là: C
Ta có: A(−2; −1; 4), B(1; −3; −1)
⇒ 
= (1 – (−2); −3 – (−1); −1 – 4) = (3; −2; −5).
Vậy = (3; −2; −5).
Lời giải
Đáp án đúng là: A
Gọi điểm C(x; y; z).
Có 
= (x – (−1); y – (−1); z – 1) = (x + 1; y + 1; z – 1).
hay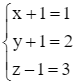 
⇒ 
.
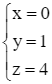Vậy C(0; 1; 4).
Lời giải
|
a) Đ |
b) S |
c) Đ |
d) S |
Ta có: 
= (1 – 1; −1 – 0; 1 – 1) = (0; −1; 0).
Có B(xB; yB; zB), C(4; 5; −5) nên 
= (4 − xB; 5 − yB; −5 − zB).
Trong hình hộp ABCD.A'B'C'D', ta có: 
(hai vectơ cùng hướng và BC = A'D').
Có với = (4 − xB; 5 − yB; −5 − zB); = (0; −1; 0) ta được:
⇔ 
.
Vậy tọa độ điểm B là (4; 6; −5).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8/8
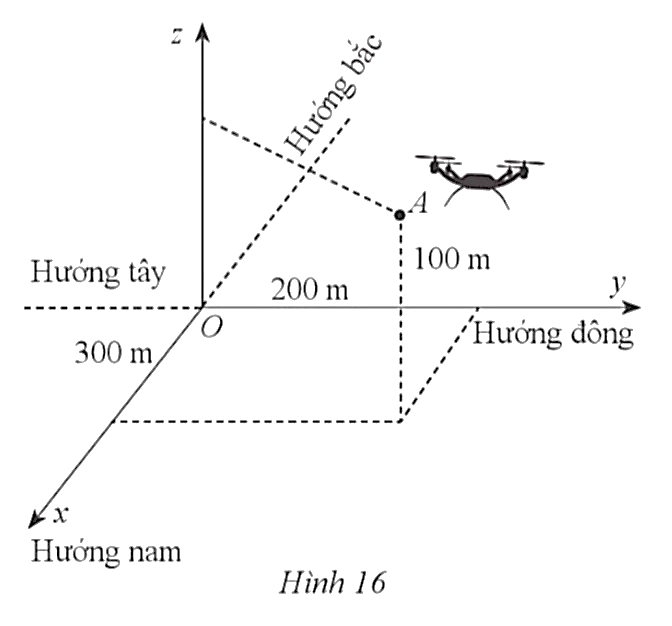
Trong quá trình cất cánh của một máy bay không người lái: Ban đầu máy bay ở vị trí A, máy bay cách vị trí điều khiển 300 m về phía nam và 200 m về phía đông, đồng thời cách mặt đất 100 m (Hình 16). Một phút sau, máy bay ở vị trí B cách vị trí điều khiển 1 200 m về phía nam và 2 100 m về phía đông, đồng thời cách mặt đất 250 m.
Chọn hệ trục tọa độ Oxyz với gốc tọa độ O trùng với vị trí điều khiển, mặt phẳng (Oxy) trùng với mặt đất, trục Ox có hướng trùng với hướng nam, trục Oy có hướng trùng với hướng đông, trục Oz vuông góc với mặt đất hướng lên bầu trời, mỗi đơn vị trên trục tương ứng với 1 m. Hãy xác định tọa độ vectơ dịch chuyển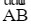 
của máy bay không người lái đó.
Trong quá trình cất cánh của một máy bay không người lái: Ban đầu máy bay ở vị trí A, máy bay cách vị trí điều khiển 300 m về phía nam và 200 m về phía đông, đồng thời cách mặt đất 100 m (Hình 16). Một phút sau, máy bay ở vị trí B cách vị trí điều khiển 1 200 m về phía nam và 2 100 m về phía đông, đồng thời cách mặt đất 250 m.
Chọn hệ trục tọa độ Oxyz với gốc tọa độ O trùng với vị trí điều khiển, mặt phẳng (Oxy) trùng với mặt đất, trục Ox có hướng trùng với hướng nam, trục Oy có hướng trùng với hướng đông, trục Oz vuông góc với mặt đất hướng lên bầu trời, mỗi đơn vị trên trục tương ứng với 1 m. Hãy xác định tọa độ vectơ dịch chuyển của máy bay không người lái đó.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Xem tiếp với tài khoản VIP
Còn 2/8 câu hỏi, đáp án và lời giải chi tiết.
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập