Giải SBT Toán 12 CD Bài tập cuối chương 3 có đáp án
34 người thi tuần này 4.6 289 lượt thi 7 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Danh sách câu hỏi:
Lời giải
Đáp án đúng là: C
Khoảng biến thiên của mẫu số liệu ghép nhóm trên là: R = 175 – 155 = 20 (cm).
Lời giải
Đáp án đúng là: B
Khoảng tứ phân vị của mẫu số liệu ghép nhóm là: ∆Q = Q3 – Q1.
Lời giải
|
a) S |
b) Đ |
c) Đ |
d) Đ |
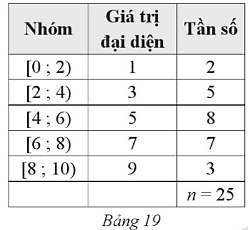
Trong mẫu số liệu ghép nhóm trên, ta có: đầu mút trái của nhóm 1 là a1 = 0, đầu mút phải của nhóm 5 là a6 = 10.
Vậy khoảng biến thiên của mẫu số liệu ghép nhóm đó là:
R = a6 – a1 = 10 – 0 = 10.
Số trung bình cộng của mẫu số liệu ghép nhóm trên là:
![]() =
= 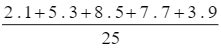 = 5,32.
= 5,32.
Phương sai của mẫu số liệu ghép nhóm trên là:
s2 = ![]() [2 . (1 – 5,32)2 + 5 . (3 – 5,32)2 + 8 . (5 – 5,32)2 + 7 . (7 – 5,32)2 + 3 . (9 – 5,32)2]
[2 . (1 – 5,32)2 + 5 . (3 – 5,32)2 + 8 . (5 – 5,32)2 + 7 . (7 – 5,32)2 + 3 . (9 – 5,32)2]
= 5,0176.
Độ lệch chuẩn của mẫu số liệu ghép nhóm đó là: s = ![]() = 2,24.
= 2,24.
Lời giải
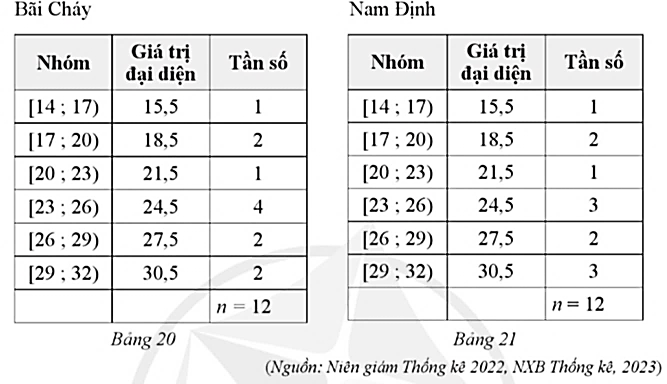
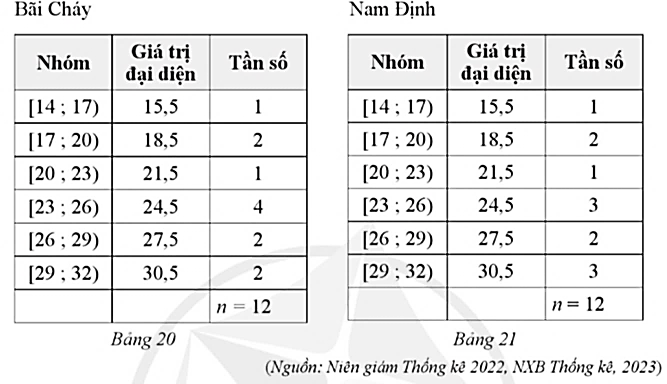
Đối với mẫu số liệu ghép nhóm ở Bảng 20 của Bãi Cháy, ta có:
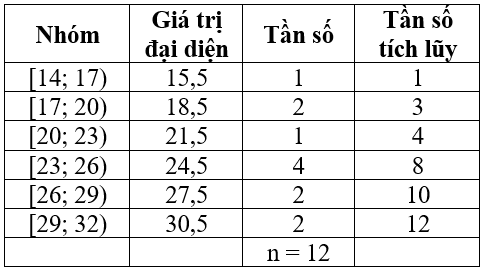
Khoảng biến thiên: R = 32 – 14 = 18.
Có 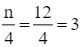 nên nhóm 2 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 3.
nên nhóm 2 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 3.
Do đó, Q1 = 17 + 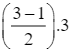 = 20.
= 20.
Có 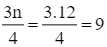 nên nhóm 5 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 9.
nên nhóm 5 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 9.
Do đó, Q3 = 26 + 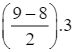 = 27,5.
= 27,5.
Suy ra khoảng tứ phân vị: ∆Q = Q3 – Q1 = 27,5 – 20 = 7,5.
Số trung bình cộng: ![]() =
= 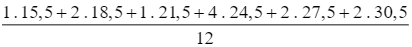 = 24.
= 24.
Phương sai:
![]() =
= ![]() [1 . (15,5 – 24)2 + 2 . (18,5 – 24)2 + 1 . (21,5 – 24)2 + 4 . (24,5 – 24)2
[1 . (15,5 – 24)2 + 2 . (18,5 – 24)2 + 1 . (21,5 – 24)2 + 4 . (24,5 – 24)2
+ 2 . (27,5 – 24)2 + 2 . (30,5 – 24)2] = 20,75.
Độ lệch chuẩn: s1 = ![]() ≈ 4,5552.
≈ 4,5552.
Đối với mẫu số liệu ghép nhóm ở Bảng 21 của Nam Định, ta có:
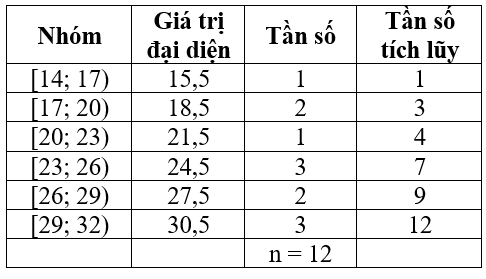
Khoảng biến thiên: R' = 32 – 14 = 18.
Có 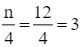 nên nhóm 2 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 3.
nên nhóm 2 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 3.
Do đó, Q'1 = 17 + 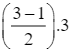 = 20.
= 20.
Có 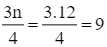 nên nhóm 5 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 9. Do đó, Q'3 = 26 +
nên nhóm 5 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 9. Do đó, Q'3 = 26 + 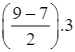 = 29.
= 29.
Suy ra khoảng tứ phân vị: ∆Q' = Q'3 – Q'1 = 29 – 20 = 9.
Số trung bình cộng: ![]() =
= 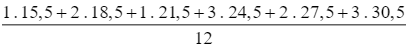 = 24,5.
= 24,5.
Phương sai:
![]() =
= ![]() [1 . (15,5 – 24,5)2 + 2 . (18,5 – 24,5)2 + 1 . (21,5 – 24,5)2 + 3 . (24,5 – 24,5)2
[1 . (15,5 – 24,5)2 + 2 . (18,5 – 24,5)2 + 1 . (21,5 – 24,5)2 + 3 . (24,5 – 24,5)2
+ 2 . (27,5 – 24,5)2 + 3 . (30,5 – 24,5)2] = 24.
Độ lệch chuẩn: s2 = ![]() ≈ 4,899.
≈ 4,899.
Vậy ta có bảng sau:
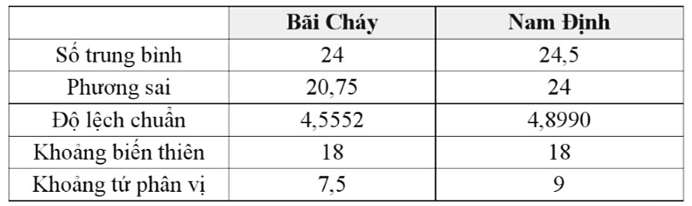
Lời giải
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.