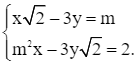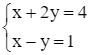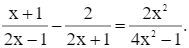Câu hỏi trong đề: Giải SGK Toán 9 KNTT Bài tập ôn tập cuối năm có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Với 
ta có hệ phương trình: 
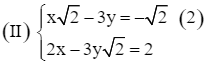
Nhân hai vế của phương trình (2) với 
ta được hệ phương trình sau:
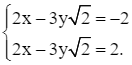
Trừ từng vế hai phương trình của hệ mới, ta được:
0x + 0y = –4. Phương trình này vô nghiệm.
Vậy hệ phương trình (II) vô nghiệm.
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Giải hệ phương trình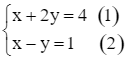 
Trừ từng vế của hai phương trình (1) và (2), ta được:
(x + 2y) – (x – y) = 4 – 1 hay 3y = 3, suy ra y = 1.
Thế y = 1 vào phương trình (2), ta được:
x – 1 = 1 hay x = 2.
Do đó hệ phương trình trên có nghiệm là (2; 1).
Vậy toạ độ giao điểm của hai đường thẳng (d1) và (d2) là điểm (2; 1).
Lời giải
Gọi x, y (triệu đồng) lần lượt là số tiền dự tính phải trả vật liệu và công thợ cho mỗi mét vuông xây dựng (0 < x < 600, 0 < y < 600).
+ Theo dự tính, tổng diện tích xây dựng là khoảng 100 m2 nên:
⦁ số tiền dùng để trả vật liệu là: 100x (triệu đồng);
⦁ số tiền dùng để trả công thợ là: 100y (triệu đồng).
Do tổng chi phí (tiền vật liệu và tiền công thợ) chú Ba dự tính hết khoảng 600 triệu đồng nên ta có phương trình:
100x + 100y = 600 hay x + y = 6. (1)
+ Theo thực tế:
⦁ tổng diện tích xây dựng là: 100 + 20 = 120 (m2);
⦁ chi phí tiền vật liệu cho mỗi mét vuông là:
(100% + 10%).x = 1,1x (triệu đồng);
⦁ tiền công thợ cho mỗi mét vuông là:
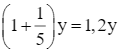(triệu đồng);
⦁ số tiền dùng để trả vật liệu là: 120.1,1x = 132x (triệu đồng);
⦁ số tiền dùng để trả công thợ là: 120.1,2y = 144y (triệu đồng).
Do tổng chi phí thực tế là 804 triệu đồng nên ta có phương trình:
132x + 144y = 804 hay 11x + 12y = 67. (2)
Từ (1) và (2) ta có hệ phương trình: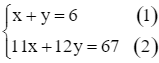 
Nhân hai vế của phương trình (1) với 12, ta được hệ phương trình sau:
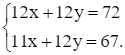
Trừ từng vế của hai phương trình trong hệ mới, ta được: x = 5.
Thế x = 5 vào phương trình (1), ta được: 5 + y = 6, suy ra y = 1.
Các giá trị x, y tìm được ở trên đều thỏa mãn điều kiện.
Vậy thực tế chú Ba phải trả 1,1.5 = 5,5 triệu đồng tiền vật liệu và 1,2.1 = 1,2 triệu đồng tiền công thợ cho mỗi mét vuông xây dựng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
-
123 bài tập Nón trụ cầu và hình khối có lời giải
-
Đề thi minh họa TS vào 10 năm học 2025 - 2026_Môn Toán_Tỉnh Đắk Lắk
-
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
-
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
-
15 câu Trắc nghiệm Toán 9 Kết nối tri thức Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
-
Bộ 10 đề thi cuối kì 1 Toán 9 Kết nối tri thức có đáp án - Đề 01
-
Tổng hợp các bài toán thực tế ôn thi vào 10 Toán 9 có đáp án (Phần 2: Hình học)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận