Sử dụng công thức tính bán kính hạt nhân \(R = 1,2 \cdot {10^{ - 15}} \cdot {A^{1/3}}(\;{\rm{m}})\) để tính gần đúng bán kính, thể tích và khối lượng riêng của hạt nhân barium \(_{56}^{138}{\rm{Ba}}.\)
Sử dụng công thức tính bán kính hạt nhân \(R = 1,2 \cdot {10^{ - 15}} \cdot {A^{1/3}}(\;{\rm{m}})\) để tính gần đúng bán kính, thể tích và khối lượng riêng của hạt nhân barium \(_{56}^{138}{\rm{Ba}}.\)
Quảng cáo
Trả lời:
Bán kính: \(R = 6,2 \cdot {10^{ - 15}}\;{\rm{m}}.\)
Thể tích: \(V = \frac{4}{3}\pi {R^3} = \frac{4}{3}\pi {\left( {1,{{2.10}^{ - 15}}} \right)^3}A = 1,{0.10^{ - 42}}\;{{\rm{m}}^3}.\)
Khối lượng riêng: \(D = \frac{m}{V} = \frac{{A\left( {1,{{66054.10}^{ - 27}}\;{\rm{kg}}} \right)}}{{\frac{4}{3}\pi {{\left( {1,{{2.10}^{ - 15}}\;{\rm{m}}} \right)}^3}A}} = 2,{3.10^{17}}\;{\rm{kg}}/{{\rm{m}}^3}.\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
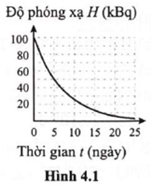
A. 5 ngày.
B. \(0,137\;{{\rm{s}}^{ - 1}}.\)
Lời giải
Chọn đáp án C
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.