Câu hỏi:
12/07/2024 15,320
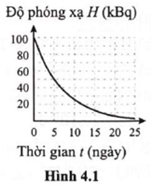
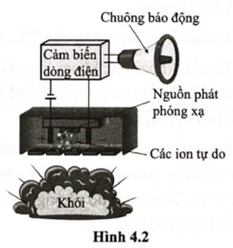
Hình 4.2 mô tả sơ đồ hoạt động đơn giản hoá của cảm biến báo khói ion hoá. Nguồn phóng xạ \(\alpha \) americium \(_{95}^{241}{\rm{Am}}\) có hằng số phóng xạ \(5,081 \cdot {10^{ - 11}}\;{{\rm{s}}^{ - 1}}\) được đặt giữa hai bản kim loại kết nối với một pin. Các hạt \(\alpha \) phóng ra làm ion hoá không khí giữa hai bản kim loại, cho phép một dòng điện nhỏ chạy giữa hai bản kim loại đó và chuông báo không kêu.
Nếu có khói bay vào giữa hai bản kim loại, các ion trong này sẽ kết hợp với những phân tử khói và dịch chuyển chậm hơn làm cường độ dòng điện chạy giữa hai bản kim loại giảm đi. Khi dòng điện giảm tới mức nhất định thì cảm biến báo khói sẽ gửi tín hiệu kích hoạt chuông báo cháy. Các ý a), b), c), d) dưới đây là đúng hay sai?
a) Tia \(\alpha \) phát ra từ nguồn phóng xạ bị lệch về phía bản kim loại nhiễm điện dương.
Hình 4.2 mô tả sơ đồ hoạt động đơn giản hoá của cảm biến báo khói ion hoá. Nguồn phóng xạ \(\alpha \) americium \(_{95}^{241}{\rm{Am}}\) có hằng số phóng xạ \(5,081 \cdot {10^{ - 11}}\;{{\rm{s}}^{ - 1}}\) được đặt giữa hai bản kim loại kết nối với một pin. Các hạt \(\alpha \) phóng ra làm ion hoá không khí giữa hai bản kim loại, cho phép một dòng điện nhỏ chạy giữa hai bản kim loại đó và chuông báo không kêu.
Nếu có khói bay vào giữa hai bản kim loại, các ion trong này sẽ kết hợp với những phân tử khói và dịch chuyển chậm hơn làm cường độ dòng điện chạy giữa hai bản kim loại giảm đi. Khi dòng điện giảm tới mức nhất định thì cảm biến báo khói sẽ gửi tín hiệu kích hoạt chuông báo cháy. Các ý a), b), c), d) dưới đây là đúng hay sai?
a) Tia \(\alpha \) phát ra từ nguồn phóng xạ bị lệch về phía bản kim loại nhiễm điện dương.
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Tia \(\alpha \) mang điện tích dương nên bị lệch về phía bản kim loại nhiễm điện âm.
=> Sai
Câu hỏi cùng đoạn
Câu 2:
b) Chu kì bán rã của americium \(_{95}^{241}{\rm{Am}}\) là \(1,{58.10^5}\) ngày.
b) Chu kì bán rã của americium \(_{95}^{241}{\rm{Am}}\) là \(1,{58.10^5}\) ngày.
Lời giải của GV VietJack
b) \(T = \frac{{\ln 2}}{\lambda } = 1,{58.10^5}\) ngày.
=> Đúng
Câu 3:
c) Độ phóng xạ của nguồn americium \(_{95}^{241}{\rm{Am}}\) có khối lượng \(0,125\mu {\rm{g}}\) là \(25,7{\rm{kBq}}.\)
c) Độ phóng xạ của nguồn americium \(_{95}^{241}{\rm{Am}}\) có khối lượng \(0,125\mu {\rm{g}}\) là \(25,7{\rm{kBq}}.\)
Lời giải của GV VietJack
c) \({H_0} = \lambda {N_0} = 15,9 \cdot {10^3}\;{\rm{Bq}}.\)
=> Sai
Câu 4:
d) Sau khi sử dụng 15 năm, độ phóng xạ của nguồn americium \(_{95}^{241}{\rm{Am}}\) trong cảm biến giảm còn 3,47% so với độ phóng xạ ban đầu lúc mới mua.
d) Sau khi sử dụng 15 năm, độ phóng xạ của nguồn americium \(_{95}^{241}{\rm{Am}}\) trong cảm biến giảm còn 3,47% so với độ phóng xạ ban đầu lúc mới mua.
Lời giải của GV VietJack
d) \(H = {H_0}{2^{ - \lambda t}} = 97,6\% {H_0}.\)
=> Sai
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới)
Đã bán 1,5k
₫ 70.000
₫ 36.000
Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết)
Đã bán 986
₫ 70.000
₫ 36.000
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Hình 4.1 biểu diễn sự thay đổi độ phóng xạ của một mẫu chất phóng xạ theo thời gian. Hằng số phóng xạ của chất này là
Hình 4.1 biểu diễn sự thay đổi độ phóng xạ của một mẫu chất phóng xạ theo thời gian. Hằng số phóng xạ của chất này là
Xem đáp án »
12/07/2024
29,074
Câu 2:
Nếu mỗi hạt nhân \(^{235}{\rm{U}}\) phân hạch giải phóng trung bình \(200,0{\rm{MeV}}\) thì năng lượng toả ra khi \(2,50\;{{\rm{g}}^{235}}{\rm{U}}\) phân hạch hoàn toàn có thể thắp sáng một bóng đèn \(100\;{\rm{W}}\) trong bao lâu? (Kết quả tính theo đơn vị năm và lấy đến một chữ số sau dấu phẩy thập phân).
Nếu mỗi hạt nhân \(^{235}{\rm{U}}\) phân hạch giải phóng trung bình \(200,0{\rm{MeV}}\) thì năng lượng toả ra khi \(2,50\;{{\rm{g}}^{235}}{\rm{U}}\) phân hạch hoàn toàn có thể thắp sáng một bóng đèn \(100\;{\rm{W}}\) trong bao lâu? (Kết quả tính theo đơn vị năm và lấy đến một chữ số sau dấu phẩy thập phân).
Xem đáp án »
12/07/2024
27,723
Câu 3:
Một phòng thí nghiệm nhập về lượng đồng phóng xạ nguyên chất \(^{64}{\rm{Cu}}\) có khối lượng ban đầu là \(55\;{\rm{g}}.\) Chu kì bán rã của đồng vị này là 12,7 giờ. Tính khối lượng \(^{64}{\rm{Cu}}\) đã bị phân rã trong ngày thứ 10 kể từ lúc nhập về. (Kết quả tính có đơn vị là \({\rm{mg}}\) và lấy một chữ số sau dấu phẩy thập phân).
Một phòng thí nghiệm nhập về lượng đồng phóng xạ nguyên chất \(^{64}{\rm{Cu}}\) có khối lượng ban đầu là \(55\;{\rm{g}}.\) Chu kì bán rã của đồng vị này là 12,7 giờ. Tính khối lượng \(^{64}{\rm{Cu}}\) đã bị phân rã trong ngày thứ 10 kể từ lúc nhập về. (Kết quả tính có đơn vị là \({\rm{mg}}\) và lấy một chữ số sau dấu phẩy thập phân).
Xem đáp án »
12/07/2024
22,839
Câu 4:
Potassium (kali) là nguyên tố dinh dưỡng khoáng thiết yếu đối với cây trồng. Trong potassium tự nhiên có 0,0117% là đồng vị phóng xạ̣ \(_{19}^{40}\;{\rm{K}}\) với chu kì bán rã là \(1,{25.10^9}\) năm.
a) Xác định độ phóng xạ của \(_{19}^{40}\;{\rm{K}}\) trong mỗi gam potassium tự nhiên.
b) Chuối, khoai tây, khoai lang là những thực phẩm có hàm lượng potassium cao. Một quả chuối trung bình chứa khoảng \(450{\rm{mg}}\) potassium. Xác định độ phóng xạ của lượng potassium đó.
c) Potassium cũng là một trong những khoáng chất cần thiết cho cơ thể con người. Hàm lượng potassium trung bình trên mỗi kilogam cơ thể người trưởng thành là \(2,5\;{\rm{g}}/{\rm{kg}}.\) Xác định độ phóng xạ của \(_{19}^{40}\;{\rm{K}}\) trong cơ thể một người trưởng thành có khối lượng \(65\;{\rm{kg}}.\)
Potassium (kali) là nguyên tố dinh dưỡng khoáng thiết yếu đối với cây trồng. Trong potassium tự nhiên có 0,0117% là đồng vị phóng xạ̣ \(_{19}^{40}\;{\rm{K}}\) với chu kì bán rã là \(1,{25.10^9}\) năm.
a) Xác định độ phóng xạ của \(_{19}^{40}\;{\rm{K}}\) trong mỗi gam potassium tự nhiên.
b) Chuối, khoai tây, khoai lang là những thực phẩm có hàm lượng potassium cao. Một quả chuối trung bình chứa khoảng \(450{\rm{mg}}\) potassium. Xác định độ phóng xạ của lượng potassium đó.
c) Potassium cũng là một trong những khoáng chất cần thiết cho cơ thể con người. Hàm lượng potassium trung bình trên mỗi kilogam cơ thể người trưởng thành là \(2,5\;{\rm{g}}/{\rm{kg}}.\) Xác định độ phóng xạ của \(_{19}^{40}\;{\rm{K}}\) trong cơ thể một người trưởng thành có khối lượng \(65\;{\rm{kg}}.\)
Xem đáp án »
12/07/2024
17,771
Câu 5:
Cho ba hạt nhân X, Y, Z có các đặc điểm sau:
Hạt nhân X có 9 proton và 10 neutron.
Hạt nhân Y có tất cả 20 nucleon trong đó có 11 nucleon trung hoà.
Hạt nhân Z có 10 nucleon mang điện và 10 nucleon trung hoà.
Trong các phát biểu dưới đây, phát biểu nào là đúng, phát biểu nào là sai?
a) X và Y là hai hạt nhân đồng vị.
b) X và Z có cùng điện tích.
c) Y và Z có cùng số khối.
d) T và Z có bán kính xấp xỉ bằng nhau.
Cho ba hạt nhân X, Y, Z có các đặc điểm sau:
Hạt nhân X có 9 proton và 10 neutron.
Hạt nhân Y có tất cả 20 nucleon trong đó có 11 nucleon trung hoà.
Hạt nhân Z có 10 nucleon mang điện và 10 nucleon trung hoà.
Trong các phát biểu dưới đây, phát biểu nào là đúng, phát biểu nào là sai?
a) X và Y là hai hạt nhân đồng vị.
b) X và Z có cùng điện tích.
c) Y và Z có cùng số khối.
d) T và Z có bán kính xấp xỉ bằng nhau.
Xem đáp án »
12/07/2024
17,411
Câu 6:
Trong \(102\;{\rm{g}}_{29}^{63}{\rm{Cu}},\) số hạt neutron nhiều hơn số hạt proton là
Xem đáp án »
12/07/2024
16,767
Câu 7:
Đồng vị \(^{238}{\rm{U}}\) phân rã qua một chuỗi phân rã phóng xạ \(\alpha \) và \(\beta \) biến thành hạt nhân bền \(^{206}\;{\rm{Pb}}.\) Biết chu kì bán rã của \(^{238}{\rm{U}}\) là \(4,47 \cdot {10^9}\) năm. Một khối đá được phát hiện chứa \(46,97{\rm{m}}{{\rm{g}}^{238}}{\rm{U}}\) và \(23,15{\rm{m}}{{\rm{g}}^{206}}\;{\rm{Pb}}.\) Giả sử khối đá khi mới hình thành không chứa nguyên tố chì và tất cả lượng chì có mặt trong đó đều là sản phẩm phân rã của \(^{238}{\rm{U}}.\) Tuổi của khối đá đó là bao nhiêu tỉ năm? (Kết quả lấy đến một chữ số sau dấu thập phân).
Đồng vị \(^{238}{\rm{U}}\) phân rã qua một chuỗi phân rã phóng xạ \(\alpha \) và \(\beta \) biến thành hạt nhân bền \(^{206}\;{\rm{Pb}}.\) Biết chu kì bán rã của \(^{238}{\rm{U}}\) là \(4,47 \cdot {10^9}\) năm. Một khối đá được phát hiện chứa \(46,97{\rm{m}}{{\rm{g}}^{238}}{\rm{U}}\) và \(23,15{\rm{m}}{{\rm{g}}^{206}}\;{\rm{Pb}}.\) Giả sử khối đá khi mới hình thành không chứa nguyên tố chì và tất cả lượng chì có mặt trong đó đều là sản phẩm phân rã của \(^{238}{\rm{U}}.\) Tuổi của khối đá đó là bao nhiêu tỉ năm? (Kết quả lấy đến một chữ số sau dấu thập phân).
Xem đáp án »
12/07/2024
16,190
🔥 Đề thi HOT:
-
83 câu Trắc nghiệm Vật lý 12 Cánh diều Chủ đề 4: Vật lý hạt nhân
-
62 câu Trắc nghiệm Vật lý 12 Cánh diều Chủ đề 3: Từ trường có đáp án
-
56 câu Trắc nghiệm Vật lý 12 Cánh diều Chủ đề 2: Khí lý tưởng
-
91 câu Trắc nghiệm Vật lý 12 Cánh diều Chủ đề 1: Vật lý nhiệt
-
1000 câu hỏi lý thuyết trọng tâm môn Vật Lý lớp 12 có đáp án
-
2 câu Trắc nghiệm Dao động cơ học cơ bản
-
21 câu Trắc nghiệm Vật lý 12 Kết nối tri thức Bài 1. Cấu trúc của chất. Sự chuyển thể có đáp án
-
2020 câu Trắc nghiệm tổng hợp Vật lí 2023 có đáp án (Phần 2)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận