Sử dụng sơ đồ ở Hình 9.3, tính năng lượng cần thiết để nguyên tử hydrogen chuyển từ trạng thái cơ bản đến trạng thái có năng lượng bằng 0 (năng lượng ion hoá nguyên tử).

Sử dụng sơ đồ ở Hình 9.3, tính năng lượng cần thiết để nguyên tử hydrogen chuyển từ trạng thái cơ bản đến trạng thái có năng lượng bằng 0 (năng lượng ion hoá nguyên tử).

Quảng cáo
Trả lời:
Năng lượng cần thiết để nguyên tử hydrogen chuyển từ trạng thái cơ bản đến trạng thái có năng lượng bằng không (năng lượng ion hoá nguyên tử):
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Ta có: \[\varepsilon = {E_n} - {E_m} \Rightarrow {E_n} = \varepsilon + {E_m} = 12,09 - 13,6 = - 1,51\,eV\]
Mà \[{E_n} = - \frac{{13,6}}{{{n^2}}} = - 1,51 \Rightarrow n \approx 3\]. Khi đó nguyên tử sẽ ở mức M
\[\varepsilon = \frac{{hc}}{\lambda } \Rightarrow {12,09.1,6.10^{ - 19}} = \frac{{{{6,625.10}^{ - 34}}{{.3.10}^8}}}{\lambda } \Rightarrow \lambda = {10^{ - 7}}\,m\]
Lời giải
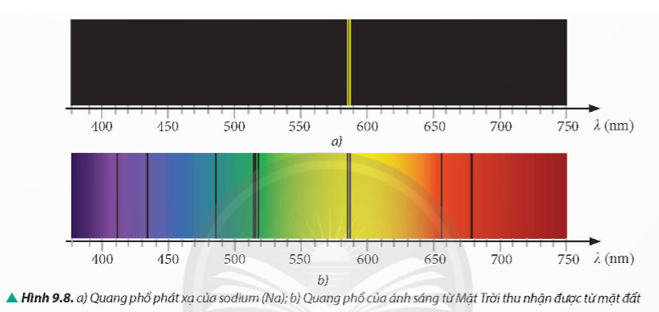
Sự xuất hiện các vạch tối trên nền màu liên tục trong Hình 9.8b vì: Vạch tối xuất hiện do hiện tượng hấp thụ ánh sáng. Ánh sáng từ Mặt Trời (gồm nhiều bước sóng khác nhau) đi qua khí quyển Trái Đất. Các nguyên tử hydrogen và sodium trong khí quyển hấp thụ một phần ánh sáng với các bước sóng nhất định tương ứng với các mức năng lượng của chúng khiến các bước sóng đó không thể đến được Trái Đất, tạo nên các vạch tối trên nền màu liên tục.
Các vạch tối này, ta có thể khẳng định trong khí quyển quanh Trái Đất có tồn tại nguyên tử hydrogen (H) và nguyên tử sodium (Na) vì:
Dựa trên vạch D: Vạch D màu vàng trong quang phổ ánh sáng mặt trời cho thấy sự tồn tại của nguyên tử sodium trong khí quyển Trái Đất.
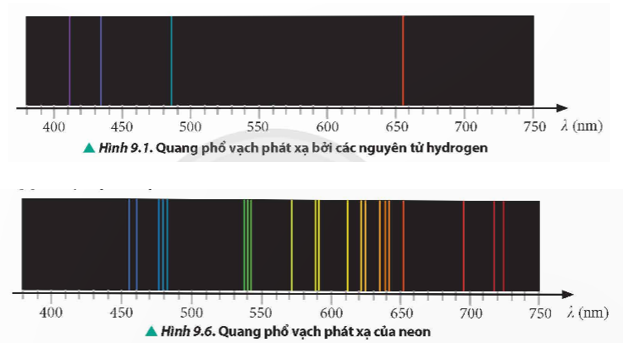
Dựa trên các vạch tối khác: So sánh vị trí các vạch tối trong quang phổ ánh sáng mặt trời với vị trí các vạch sáng trong quang phổ phát xạ của hydrogen. Nếu trùng khớp, khẳng định sự tồn tại của nguyên tử hydrogen trong khí quyển Trái Đất.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.