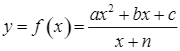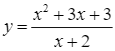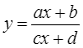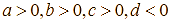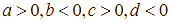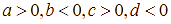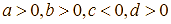Cho một tấm nhôm hình vuông cạnh 12 cm, người ta cắt ở bốn góc bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng 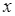 (cm), rồi gập tấm nhôm lại để được một cái hộp có dạng hình hộp chữ nhật không có nắp (tham khảo hình vẽ).
(cm), rồi gập tấm nhôm lại để được một cái hộp có dạng hình hộp chữ nhật không có nắp (tham khảo hình vẽ).
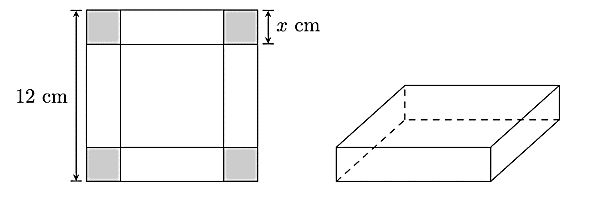
Giá trị của 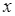 bằng bao nhiêu centimét để thể tích của khối hộp đó là lớn nhất?
bằng bao nhiêu centimét để thể tích của khối hộp đó là lớn nhất?
Cho một tấm nhôm hình vuông cạnh 12 cm, người ta cắt ở bốn góc bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng ![]() (cm), rồi gập tấm nhôm lại để được một cái hộp có dạng hình hộp chữ nhật không có nắp (tham khảo hình vẽ).
(cm), rồi gập tấm nhôm lại để được một cái hộp có dạng hình hộp chữ nhật không có nắp (tham khảo hình vẽ).

Giá trị của ![]() bằng bao nhiêu centimét để thể tích của khối hộp đó là lớn nhất?
bằng bao nhiêu centimét để thể tích của khối hộp đó là lớn nhất?
Câu hỏi trong đề: Bộ 10 đề thi giữa kì 1 Toán 12 Kết nối tri thức có đáp án !!
Quảng cáo
Trả lời:
Ta thấy độ dài ![]() (cm) của cạnh hình vuông bị cắt phải thỏa mãn điều kiện 0 < x < 6.
(cm) của cạnh hình vuông bị cắt phải thỏa mãn điều kiện 0 < x < 6.
Khi đó, thể tích của khối hộp là:
![]() với
với ![]() .
.
Ta có: ![]() ,
, ![]() hoặc
hoặc ![]() .
.
Bảng biến thiên của hàm số ![]() như sau:
như sau:
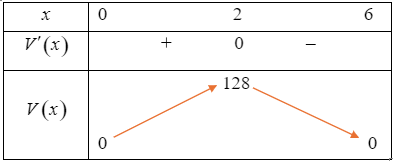
Căn cứ vào bảng biến thiên, ta thấy trên khoảng ![]() , hàm số
, hàm số ![]() đạt giá trị lớn nhất bằng
đạt giá trị lớn nhất bằng ![]() tại
tại ![]() . Vậy để khối hộp tạo thành có thể tích lớn nhất thì
. Vậy để khối hộp tạo thành có thể tích lớn nhất thì ![]() (cm).
(cm).
Đáp số: ![]() .
.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
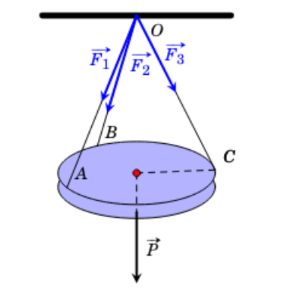
Gọi ![]() lần lượt là các điểm sao cho
lần lượt là các điểm sao cho ![]() . Lấy các điểm
. Lấy các điểm ![]() sao cho
sao cho ![]() là hình hộp như hình dưới đây.
là hình hộp như hình dưới đây.
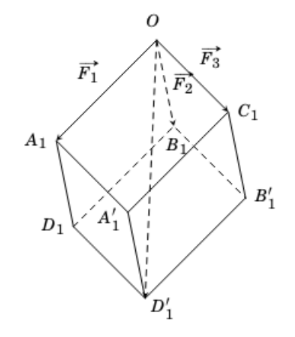
Theo quy tắc hình hộp, ta có: ![]() .
.
Mặt khác, do các lực căng ![]() đôi một vuông góc và
đôi một vuông góc và ![]() (N) nên hình hộp
(N) nên hình hộp ![]() có ba cạnh
có ba cạnh ![]() đôi một vuông góc và bằng nhau.
đôi một vuông góc và bằng nhau.
Do đó, hình hộp ![]() là hình lập phương có độ dài cạnh bằng 15.
là hình lập phương có độ dài cạnh bằng 15.
Suy ra độ dài đường chéo của hình lập phương đó bằng ![]() .
.
Do chiếc đèn ở vị trí cân bằng nên ![]() , ở đó
, ở đó ![]() là trọng lực tác dụng lên chiếc đèn.
là trọng lực tác dụng lên chiếc đèn.
Vậy trọng lượng của chiếc đèn là ![]() (N).
(N).
Đáp số: ![]() .
.
Lời giải
a) S, b) Đ, c) S, d) Đ.
Hướng dẫn giải
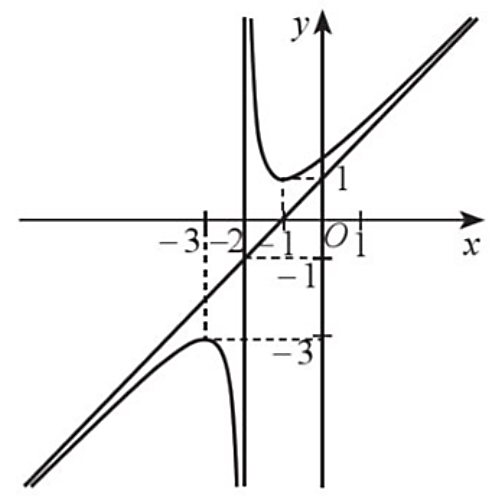
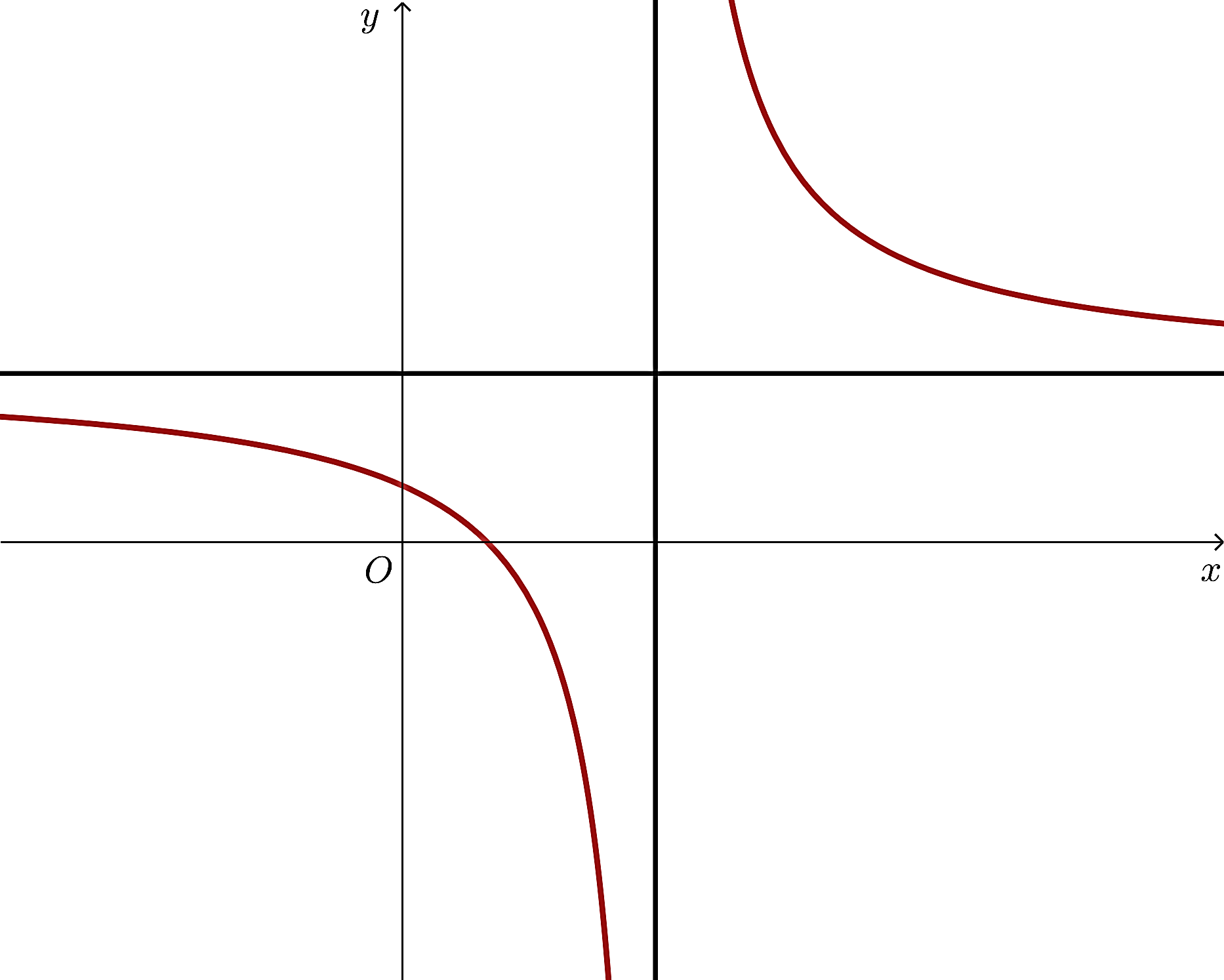
– Quan sát hình vẽ, ta thấy:
Hàm số đã cho có tập xác định là ![]() .
.
Trên các khoảng ![]() và
và ![]() , đồ thị hàm số đi lên từ trái qua phải nên hàm số đã cho đồng biến trên mỗi khoảng này.
, đồ thị hàm số đi lên từ trái qua phải nên hàm số đã cho đồng biến trên mỗi khoảng này.
Trên các khoảng ![]() và
và ![]() , đồ thị hàm số đi xuống từ trái qua phải nên hàm số đã cho nghịch biến trên mỗi khoảng này.
, đồ thị hàm số đi xuống từ trái qua phải nên hàm số đã cho nghịch biến trên mỗi khoảng này.
Vậy ý) a sai.
– Hàm số đã cho đạt cực đại tại ![]() ; đạt cực tiểu tại
; đạt cực tiểu tại ![]() , do đó ý b) đúng.
, do đó ý b) đúng.
– Tiệm cận đứng của đồ thị hàm số đã cho là đường thẳng ![]() , do đó ý c) sai.
, do đó ý c) sai.
– Vì ![]() là tiệm cận đứng nên
là tiệm cận đứng nên ![]() . Khi đó,
. Khi đó, 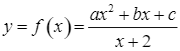 .
.
Ta có 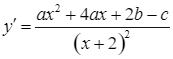 ;
; ![]() (*).
(*).
![]() là một nghiệm của phương trình (*), do đó
là một nghiệm của phương trình (*), do đó ![]() .
.
Các điểm ![]() ,
, ![]() thuộc đồ thị hàm số đã cho nên tọa độ các điểm này thỏa mãn hàm số
thuộc đồ thị hàm số đã cho nên tọa độ các điểm này thỏa mãn hàm số 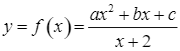 .
.
Khi đó, ta có hệ phương trình sau: 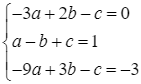
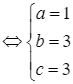 .
.
Vậy công thức xác định hàm số đã cho là 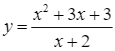 . Do đó, ý) d đúng.
. Do đó, ý) d đúng.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.