Cho hình nón có chiều cao bằng a. Biết rằng khi cắt hình nón đã cho bởi một mặt phẳng đi qua đỉnh hình nón và cách tâm của đáy hình nón một khoảng bằng \(\frac{a}{3}\), thiết diện thu được là một tam giác vuông. Thể tích của khối nón được giới hạn bởi hình nón đã cho bằng
Quảng cáo
Trả lời:
Hướng dẫn giải:
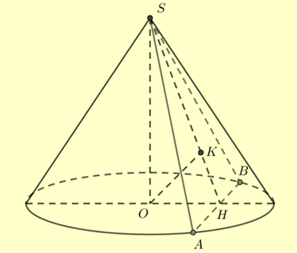
Gọi thiết diện qua đỉnh là tam giác vuông cân SAB và gọi \(H\) là trung điểm AB.
Kẻ \(OK \bot SH \Rightarrow d(O,(SAB)) = OK = \frac{a}{3}\) và ta có \(\frac{1}{{O{K^2}}} = \frac{1}{{S{O^2}}} + \frac{1}{{O{H^2}}} \Rightarrow OH = \frac{{a\sqrt 2 }}{4}\).
Do tam giác SAB vuông cân tại \(S \Rightarrow AH = SH = SH = \sqrt {S{O^2} + O{H^2}} = \frac{{3a\sqrt 2 }}{4}\).
\( \Rightarrow OA = \sqrt {O{H^2} + A{H^2}} = \frac{{a\sqrt 5 }}{2} \Rightarrow V = \frac{1}{3}\pi .O{A^2}.SO = \frac{1}{3}\pi {\left( {\frac{{a\sqrt 5 }}{2}} \right)^2}.a = \frac{{5\pi {a^3}}}{{12}}\).
Vậy thể tích của khối nón được giới hạn bởi hình nón đã cho bằng \(\frac{{5\pi {a^3}}}{{12}}\).
Chọn B
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. 741,2 m.
Lời giải
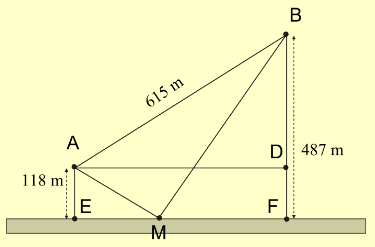
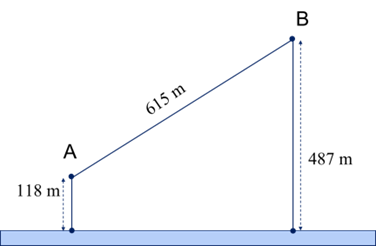
Giả sử người đó đi từ A đến M để lấy nước và đi từ M về B. Dễ dàng tính được BD = 369, EF = 492. Ta đặt EM = x, khi đó:
\(MF = 492 - x,AM = \sqrt {{x^2} + {{118}^2}} ,BM = \sqrt {{{(492 - x)}^2} + {{487}^2}} .\)
Như vậy ta có hàm số f(x) được xác định bằng tổng quãng đường AM và MB :
\(f(x) = \sqrt {{x^2} + {{118}^2}} + \sqrt {{{(492 - x)}^2} + {{487}^2}} \) với \(x \in [0;492]\)
Ta cần tìm giá trị nhỏ nhất của f(x) để có quãng đường ngắn nhất và từ đó xác định được vị trí điểm M.
\(f'(x) = \frac{x}{{\sqrt {{x^2} + {{118}^2}} }} - \frac{{492 - x}}{{\sqrt {{{(492 - x)}^2} + {{487}^2}} }}\)
\(f'(x) = 0 \Leftrightarrow \frac{x}{{\sqrt {{x^2} + {{118}^2}} }} - \frac{{492 - x}}{{\sqrt {{{(492 - x)}^2} + {{487}^2}} }} = 0\)
\( \Leftrightarrow \frac{x}{{\sqrt {{x^2} + {{118}^2}} }} = \frac{{492 - x}}{{\sqrt {{{(492 - x)}^2} + {{487}^2}} }}\)
\( \Leftrightarrow x\sqrt {{{(492 - x)}^2} + {{487}^2}} = (492 - x)\sqrt {{x^2} + {{118}^2}} \)
\( \Leftrightarrow \left\{ \begin{array}{l}{x^2}\left[ {{{(492 - x)}^2} + {{487}^2}} \right] = {\left( {492 - x} \right)^2}\left( {{x^2} + {{118}^2}} \right)\\0 \le x \le 492\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}{(487x)^2} = {(58056 - 118x)^2}\\0 \le x \le 492\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}x = \frac{{58056}}{{605}}{\rm{ hay }}x = - \frac{{58056}}{{369}}\\0 \le x \le 492\end{array} \right.\)
\( \Leftrightarrow x = \frac{{58056}}{{605}}\)
Hàm số \(f(x)\) liên tục trên đoạn [0; 492]. So sánh các giá trị của \(f(0),f\left( {\frac{{58056}}{{605}}} \right),f(492)\) ta có giá trị nhỏ nhất là \(f\left( {\frac{{58056}}{{605}}} \right) \approx 779,8\;{\rm{m}}\).
Chọn B
Câu 2
Lời giải
Chọn đáp án C
Câu 3
A. \({\rm{C}}{{\rm{H}}_3}{\rm{COOH}} + {\rm{CH}} \equiv {\rm{CH}} \to {\rm{C}}{{\rm{H}}_3}{\rm{COOCH}} = {\rm{C}}{{\rm{H}}_2}\).
B. \({\rm{C}}{{\rm{H}}_2} = {\rm{CHCOOH}} + {\rm{C}}{{\rm{H}}_3}{\rm{OH}} \to {\rm{C}}{{\rm{H}}_2} = \) \({\rm{CHCOOC}}{{\rm{H}}_3} + {{\rm{H}}_2}{\rm{O}}\).
C. \({\rm{C}}{{\rm{H}}_3}{\rm{COOH}} + {\rm{C}}{{\rm{H}}_2} = {\rm{CHOH}} \to {\rm{C}}{{\rm{H}}_3}{\rm{COOCH}} = \) \({\rm{C}}{{\rm{H}}_2} + {{\rm{H}}_2}{\rm{O}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.