Cho tam giác đều \(ABC\) có đường tròn nội tiếp \(\left( {O;r} \right)\), cắt bỏ phần hình tròn và cho hình phẳng thu được quay quanh \(AO\).
Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai?
ĐÚNG
SAI
Thể tích khối tròn xoay thu được là \(\pi {r^3}\).
Thể tích khối tròn xoay thu được bằng thể tích khối cầu có cùng bán kính với phần bị cắt bỏ.
Cho tam giác đều \(ABC\) có đường tròn nội tiếp \(\left( {O;r} \right)\), cắt bỏ phần hình tròn và cho hình phẳng thu được quay quanh \(AO\).
Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai?
|
|
ĐÚNG |
SAI |
|
Thể tích khối tròn xoay thu được là \(\pi {r^3}\). |
||
|
Thể tích khối tròn xoay thu được bằng thể tích khối cầu có cùng bán kính với phần bị cắt bỏ. |
Quảng cáo
Trả lời:
Đáp án
|
|
ĐÚNG |
SAI |
|
Thể tích khối tròn xoay thu được là \(\pi {r^3}\). |
¡ |
¤ |
|
Thể tích khối tròn xoay thu được bằng thể tích khối cầu có cùng bán kính với phần bị cắt bỏ. |
¡ |
¤ |
Phương pháp giải
- Gọi \(H\) là chân đường cao \(AH\) của tam giác \(ABC\)
- Khi quay tam giác \(ABC\) quanh trục \(AO\) ta được hình nón có thể tích là: \({V_N}\), có đáy là đường tròn đường kính \(BC\)
Lời giải
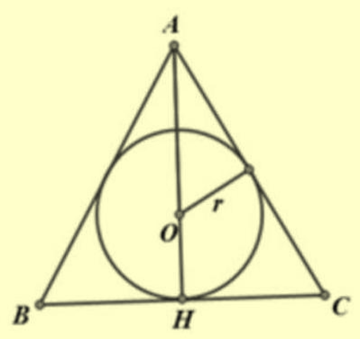
Gọi \(H\) là chân đường cao \(AH\) của tam giác \(ABC\)
Vì tam giác \(ABC\) đều nên ta có: \(AH = 3OH = 3r\), \(AH = BC\frac{{\sqrt 3 }}{2} \Leftrightarrow BC = \frac{2}{{\sqrt 3 }}AH = .r2\sqrt 3 \)
Khi quay tam giác \(ABC\) quanh trục \(AO\) ta được hình nón có thể tích là: \({V_N}\), có đáy là đường tròn đường kính \(BC\) khi đó: \({S_N} = \pi H{C^2} = \pi {r^2}3\), chiều cao của hình nón là: \(AH = 3r\), khi đó thể tích hình nón là: \({V_N} = \frac{1}{3}AH.{S_N} = \frac{1}{3}3r.\pi {r^2}3 = 3\pi {r^3}\) (đvtt)
Thể tích khối cầu khi quay hình tròn \(\left( {O;r} \right)\) quanh trục \(AO\) là: \({V_C} = \frac{4}{3}\pi {r^3}\)
Vậy thể tích \(V\) của khối tròn xoay thu được khi quay tam giác \(ABC\) đã cắt bỏ phần hình tròn quanh trục \(AO\) là: \(V = {V_N} - {V_C} = 3\pi {r^3} - \frac{4}{3}\pi {r^3} = \frac{5}{3}\pi {r^3}\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Phương pháp giải
Xét tính đúng, sai cho từng đáp án, dựa vào các công thức cộng véc tơ, độ dài véc tơ, các tính chất hai véc tơ cùng phương, hai véc tơ vuông góc.
Tọa độ véc tơ
Lời giải
\(\vec a + \vec b = \left( {2 + 1; - 2 - 1; - 4 + 1} \right) = \left( {3; - 3; - 3} \right)\) nên A đúng.
\(\vec a.\vec b = 2.1 + \left( { - 2} \right).\left( { - 1} \right) + \left( { - 4} \right).1 = 0\) nên \(\vec a \bot \vec b\) hay B đúng.
\(\left| {\vec b} \right| = \sqrt {{1^2} + {{( - 1)}^2} + {1^2}} = \sqrt 3 \) nên C đúng.
Lời giải
Đáp án: "2"
Phương pháp giải
- Tính đạo hàm và khảo sát hàm \(y = 2{x^3} - 3{x^2}\)
- Số nghiệm của phương trình đã cho bằng số giao điểm của hai đồ thị: \(\left\{ {\begin{array}{*{20}{l}}{\left( C \right):y = 2{x^3} - 3{x^2}}\\{d:y = 2m + 1}\end{array}} \right.\)
Lời giải
Xét hàm số: \(y = 2{x^3} - 3{x^2} \Rightarrow y' = 6{x^2} - 6x \Rightarrow y' = 0 \Leftrightarrow x = 0 \vee x = 1\).
Bảng biến thiên:
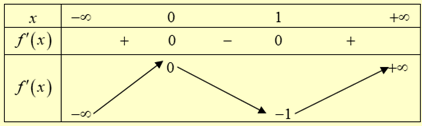
Số nghiệm của phương trình đã cho bằng số giao điểm của hai đồ thị: \(\left\{ {\begin{array}{*{20}{l}}{\left( C \right):y = 2{x^3} - 3{x^2}}\\{d \cdot y = 2m + 1}\end{array}} \right.\)
Nhìn vào bảng biến thiên ta thấy: Phương trình đã cho có hai nghiệm phân biệt
\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{2m + 1 = - 1}\\{2m + 1 = 0}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{m = - 1}\\{m = - \frac{1}{2}}\end{array} \Rightarrow S = \left\{ { - 1; - \frac{1}{2}} \right\}} \right.} \right.\).
Câu 3
A. Cụ đã tới cái tuổi được hoàn toàn nhàn rỗi để dưỡng lấy tính tình.
B. Mình chỉ là một anh nhà nho sống vào giữa buổi Tây Tàu nhố nhăng, chỉ là một kẻ chọn nhầm thế kỷ với hai bàn tay không có lợi khí mới, thì riêng lo cho thân thế, lo cho sự mất còn của mình cũng chưa xong.
C. Đủ thời giờ mà săn sóc đến hoa mới là việc khó.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.