Câu hỏi:

08/11/2024 882

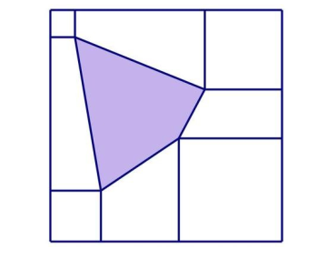
Cho hình vuông ABCD. Nối điểm chính giữa các cạnh của hình vuông ABCD ta được hình vuông EGTH. Nối điểm chính giữa các cạnh của hình vuông EGIH ta được

hình vuông MNPQ (như hình vẽ). Tổng chu vi các tam giác hơn tổng chu vi các hình vuông có trong hình là chu vi của hình nào trong hình vẽ bên?

Xem lời giải

Câu hỏi trong đề: Bộ 15 đề thi ôn vào lớp 6 môn Toán chất lượng cao năm 2024 - 2025 có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Quan sát hình vẽ ta thấy:

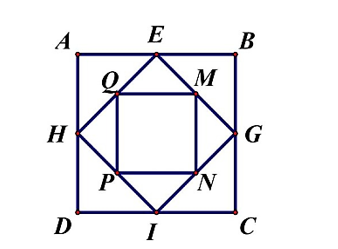
Cho hình vuông ABCD. Nối điểm chính giữa các cạnh của hình vuông ABCD ta được hình vuông (ảnh 1)

Tổng chu vi của các hình tam giác bằng tổng chu vi của: hình vuông ABCD + hình vuông MNPQ + 2 lần hình vuông EGIH.

Do đó tổng chu vi của các hình tam giác hơn tổng chu vi của các hình vuông có trong hình là chu vi của hình vuông EGIH.

Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Tính diện tích phần tô đậm, biết diện tích các hình vuông nhỏ theo chiều kim đồng hồ là 1 cm², 9 cm², 16 cm², 4 cm² và diện tích hình vuông lớn là 81cm².

Xem đáp án

Lời giải

Theo chiều kim đồng hồ, độ dài cạnh của các hình vuông có diện tích 1cm², 9cm², 16cm², 4cm² lần lượt là 1cm, 3cm, 4cm, 2cm.

Độ dài cạnh của hình vuông lớn là: 9cm.

Ta đánh số như hình vẽ sau:

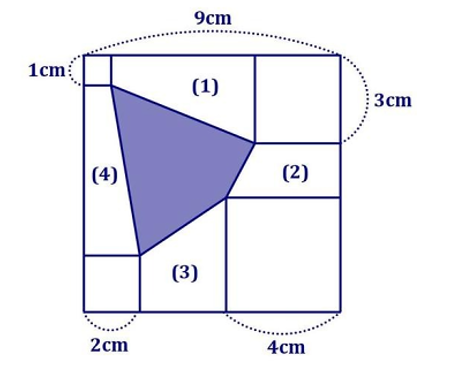
Tính diện tích phần tô đậm, biết diện tích các hình vuông nhỏ theo chiều kim đồng hồ (ảnh 2)

Quan sát hình vẽ, ta thấy các hình (1), (2), (3), (4) đều là hình thang vuông.

Chiều cao hình (1) là: 9 – 1 – 3 = 5 (cm)

Diện tích hình (1) là: (1 + 3) × 5 : 2 = 10 (cm²)

Chiều cao hình (2) là: 9 – 3 – 4 = 2(cm)

Diện tích hình (2) là: (3 + 4) × 2 : 2 = 7(cm²)

Chiều cao hình (3) là: 9 – 2 – 4 = 3 (cm)

Diện tích hình (3) là: (2 + 4) × 3 : 2 = 9 (cm²)

Chiều cao hình (4)là: 9 – 1 – 2 = 6 (cm)

Diện tích hình (4) là: (1 + 2) × 6 : 2 = 9(cm)

Diện tích hình tô đậm là: 81 – (10 + 7 + 9 + 9 + 1 + 9 + 16 + 4) = 16 (cm²)

Đáp số: 16 (cm²)

Câu 2

Cho hình thang ABCD có AB = 2cm; CD = 4cm. Chiều cao bằng trung bình cộng hai đáy. Nối AC và BD cắt nhau tại Đ.

a) Tính S_ABCD

b) Chỉ ra các cặp tam giác bằng nhau và tại sao?

c) Kéo dài DA và BC cắt nhau tại P. Tính S_ABP

Xem đáp án

Lời giải

a) Chiều cao của hình thang là: (2 + 4) : 2 = 3(mm)

Diện tích hình tháng là: (2 + 4) × 3 : 2 = 9(cm²)

b) Ta có hình vẽ sau:

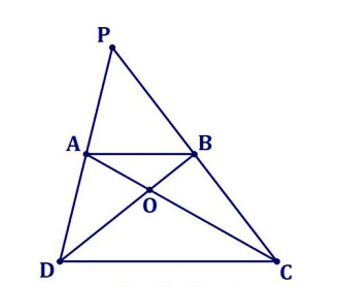
Cho hình thang ABCD có AB = 2cm; CD = 4cm. Chiều cao bằng trung bình cộng hai đáy. (ảnh 1)

+) S_ABD = S_ABC(chung cạnh đáy AB và chiều cao hạ từ đỉnh D xuống AB bằng chiều cao hạ từ đỉnh C xuống AB).

Suy ra: S_AOD + S_AOB = S_BOC + S_AOB

Vậy S_AOD = S_BOC

+) S_ADC = S_BDC (chung cạnh đáy DC và chiều cao hạ từ đỉnh A xuống DC bằng chiều cao hạ từ đỉnh B xuống DC).

Vậy ta có 3 cặp tam giác có diện tích bằng nhau là: S_ABD = S_ABC; S_AOD = S_BOC; S_ADC = S_BDC

c) Ta cóc S_ABD = $\frac{1}{2}$ × S_ADC

Vậy chiều cao hạ từ đỉnh B đến đáy AD bằng $\frac{1}{2}$ chiều cao từ đỉnh C đến đáy AD.

Suy ra: S_PAB= $\frac{1}{2}$ × S_PCA (vì chiều cao hạ từ đỉnh B đến đáy PA bằng $\frac{1}{2}$ chiều cao từ đỉnh C đến đáy AP)

Ta có: S_PAC= S_PAB + S_ABC mà S_PAB= $\frac{1}{2}$ × S_PCAnên S_PAB = S_ABC

Vậy S_PAB = S_ABC = 2 × 3 : 2 = 3 (cm²)

Câu 3

Đồng hồ Công tơ mét trên một xe ô tô chỉ 15 951 (nghĩa là ô tô đã đi được 15 951 km). Con số này đọc từ trái sang phải, hoặc ngược lại đọc từ phải sang trái đều như nhau. Khi ô tô chạy được thêm 2 giờ thì trên đồng hồ Công tơ mét lại xuất hiện một số khác có đặc điểm như trên. Hỏi trong 2 giờ trên, trung bình mỗi giờ ô tô đó chạy được bao nhiêu ki-lô-mét? Biết ô tô chạy không quá 100 km/giờ.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Kara chỉ độ nguyên chất (vàng 24 kara là vàng nguyên chất, còn 14 kara là vàng $\frac{14}{24}$ là nguyên chất). Một chiếc vòng tay 14 kara có 21 gram là vàng nguyên chất. Hỏi chiếc vòng tay nặng bao nhiêu gram?

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

a) Cho hình vuông 3 × 3. Nêu cách vẽ sao cho tô ít nhất thoả mãn cho tất cả các hình vuông 2 × 2 được tô màu ít nhất 2 ô.

b) Cho hình vuông 7 × 7. Hỏi cần tô ít nhất bao nhiêu ô sao cho trong mỗi hình vuông 4 × 4 bất kì có đúng 5 ô được tô? Giải thích vì sao?

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

An, Bắc và Cường có tổng cộng 90 cái kẹo. Số kẹo của Bắc bằng $\frac{3}{4}$ số kẹo của Cường. Số kẹo của An bằng $\frac{2}{3}$ số kẹo của Bắc. Hỏi Cường có bao nhiêu cái kẹo?

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Hỏi bài tập

Đăng ký gói thi VIP

VIP +1 tháng ( 199,000 VNĐ )

VIP +1 - Luyện thi tất cả các đề có trên Website trong 1 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +3 tháng ( 299,000 VNĐ )

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +6 tháng ( 399,000 VNĐ )

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +12 tháng ( 499,000 VNĐ )

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

Tính diện tích phần tô đậm, biết diện tích các hình vuông nhỏ theo chiều kim đồng hồ là 1 cm2, 9 cm2, 16 cm2, 4 cm2 và diện tích hình vuông lớn là 81cm2.

Cho hình thang ABCD có AB = 2cm; CD = 4cm. Chiều cao bằng trung bình cộng hai đáy. Nối AC và BD cắt nhau tại Đ. a) Tính SABCD b) Chỉ ra các cặp tam giác bằng nhau và tại sao? c) Kéo dài DA và BC cắt nhau tại P. Tính SABP

Kara chỉ độ nguyên chất (vàng 24 kara là vàng nguyên chất, còn 14 kara là vàng 1424là nguyên chất). Một chiếc vòng tay 14 kara có 21 gram là vàng nguyên chất. Hỏi chiếc vòng tay nặng bao nhiêu gram?

An, Bắc và Cường có tổng cộng 90 cái kẹo. Số kẹo của Bắc bằng 34 số kẹo của Cường. Số kẹo của An bằng 23số kẹo của Bắc. Hỏi Cường có bao nhiêu cái kẹo?

VIP +1 tháng ( 199,000 VNĐ )

VIP +3 tháng ( 299,000 VNĐ )

VIP +6 tháng ( 399,000 VNĐ )

VIP +12 tháng ( 499,000 VNĐ )

🔥 Đề thi HOT:

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Tính diện tích phần tô đậm, biết diện tích các hình vuông nhỏ theo chiều kim đồng hồ là 1 cm², 9 cm², 16 cm², 4 cm² và diện tích hình vuông lớn là 81cm².

Cho hình thang ABCD có AB = 2cm; CD = 4cm. Chiều cao bằng trung bình cộng hai đáy. Nối AC và BD cắt nhau tại Đ.

a) Tính S_ABCD

b) Chỉ ra các cặp tam giác bằng nhau và tại sao?

c) Kéo dài DA và BC cắt nhau tại P. Tính S_ABP

Kara chỉ độ nguyên chất (vàng 24 kara là vàng nguyên chất, còn 14 kara là vàng $\frac{14}{24}$ là nguyên chất). Một chiếc vòng tay 14 kara có 21 gram là vàng nguyên chất. Hỏi chiếc vòng tay nặng bao nhiêu gram?

An, Bắc và Cường có tổng cộng 90 cái kẹo. Số kẹo của Bắc bằng $\frac{3}{4}$ số kẹo của Cường. Số kẹo của An bằng $\frac{2}{3}$ số kẹo của Bắc. Hỏi Cường có bao nhiêu cái kẹo?