Trong không gian \[Oxyz\], cho \(\Delta ABC\)với \(A\left( {1\,;\,2\,;\,3} \right)\), \(B\left( {4\,;\,5\,;\,6} \right)\), \(C\left( {2\,;\,7\,;\,4} \right)\)
a) Tọa độ vectơ \(\overrightarrow {AB} = \left( {3;3;3} \right)\).
b) Tọa độ trọng tâm \(G\) của \(\Delta ABC\) là \(G\left( {\frac{7}{3};\,\frac{{14}}{3}\,;\,\frac{{13}}{3}} \right)\).
c) Tích vô hướng của hai véc tơ \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \) là 31.
d) Chu vi và diện tích của \(\Delta ABC\) lần lượt là \(8\sqrt 3 \) và \(6\sqrt 2 \,\).
Trong không gian \[Oxyz\], cho \(\Delta ABC\)với \(A\left( {1\,;\,2\,;\,3} \right)\), \(B\left( {4\,;\,5\,;\,6} \right)\), \(C\left( {2\,;\,7\,;\,4} \right)\)
a) Tọa độ vectơ \(\overrightarrow {AB} = \left( {3;3;3} \right)\).
b) Tọa độ trọng tâm \(G\) của \(\Delta ABC\) là \(G\left( {\frac{7}{3};\,\frac{{14}}{3}\,;\,\frac{{13}}{3}} \right)\).
c) Tích vô hướng của hai véc tơ \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \) là 31.
d) Chu vi và diện tích của \(\Delta ABC\) lần lượt là \(8\sqrt 3 \) và \(6\sqrt 2 \,\).
Quảng cáo
Trả lời:
a) Đ, b) Đ, c) S, d) Đ
a) \(\overrightarrow {AB} = \left( {3;3;3} \right)\).
b) Gọi \(G\) là trọng tâm của \(\Delta ABC\).
Ta có: \(G\left( {\frac{{{x_A} + {x_B} + {x_C}}}{3};\,\frac{{{y_A} + {y_B} + {y_C}}}{3}\,;\,\frac{{{z_A} + {z_B} + {z_C}}}{3}} \right)\)
Vậy: \(G\left( {\frac{7}{3};\,\frac{{14}}{3}\,;\,\frac{{13}}{3}} \right)\).
c) \(\overrightarrow {AB} = \left( {3\,;\,3\,;\,3} \right)\); \(\overrightarrow {AC} = \left( {1\,;\,5\,;\,1} \right)\).
Tích vô hướng của hai véc tơ \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \): \(\overrightarrow {AB} .\overrightarrow {AC} = 3.1 + 3.5 + 3.1 = 21\).
d) Ta có:
\(AB = \sqrt {{{(4 - 1)}^2} + {{(5 - 2)}^2} + {{(6 - 3)}^2}} = 3\sqrt 3 \)
\(BC = \sqrt {{{(2 - 4)}^2} + {{(7 - 5)}^2} + {{(4 - 6)}^2}} = 2\sqrt 3 \)
\(AC = \sqrt {{{(2 - 1)}^2} + {{(7 - 2)}^2} + {{(4 - 3)}^2}} = 3\sqrt 3 \)
Chu vi \(\Delta ABC\):
\({P_{\Delta ABC}} = AB + BC + AC = 3\sqrt 3 + 2\sqrt 3 + 3\sqrt 3 = 8\sqrt 3 \).
Ta có nửa chu vi \(\Delta ABC\) là \(p = \frac{1}{2}.8\sqrt 3 = 4\sqrt 3 \).
Áp dụng công thức Heron, ta có diện tích tam giác \(ABC\) là:
\({S_{\Delta ABC}} = \sqrt {p\left( {p - AB} \right)\left( {p - BC} \right)\left( {p - AC} \right)} \)
\( = \sqrt {4\sqrt 3 \left( {4\sqrt 3 - 3\sqrt 3 } \right)\left( {4\sqrt 3 - 2\sqrt 3 } \right)\left( {4\sqrt 3 - 3\sqrt 3 } \right)} = 6\sqrt 2 \,\).a
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) S, b) S, c) S, d) Đ
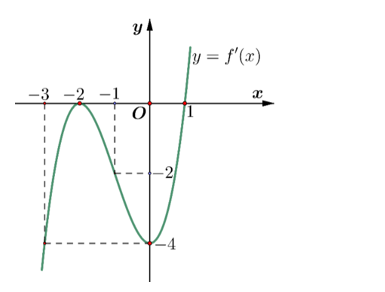
a) Vì từ đồ thị của hàm số \(y = f'\left( x \right)\) ta thấy \(f'\left( x \right) \ge 0\) với \(\forall x \ge 1\) nên hàm số đồng biến trên khoảng \(\left( {1; + \infty } \right)\).
b) Vì từ đồ thị của hàm số \(y = f'\left( x \right)\) ta thấy \(f'\left( x \right)\) chỉ đổi dấu một lần qua \(x = 1\) nên hàm số có một điểm cực trị.
c) Từ đồ thị ta có hàm số \(f'\left( x \right)\) có dạng: \(f'\left( x \right) = a{\left( {x + 2} \right)^2}\left( {x - 1} \right)\).
Đồ thị hàm số \(y = f'\left( x \right)\) đi qua \(\left( {0; - 4} \right)\) nên: \( - 4 = a{\left( {0 + 2} \right)^2}\left( {0 - 1} \right) \Leftrightarrow a = 1\).
Vậy \(f'\left( x \right) = {\left( {x + 2} \right)^2}\left( {x - 1} \right) \Rightarrow f'\left( 2 \right) = {\left( {2 + 2} \right)^2}\left( {2 - 1} \right) = 16\).
d) Ta có: \(g'\left( x \right) = f'\left( x \right) - x + 1 = 0 \Leftrightarrow f'\left( x \right) = x - 1\).
Vẽ đường thẳng \(y = x - 1\) trên cùng hệ trục tọa độ với đồ thị hàm số \(y = f'\left( x \right)\).
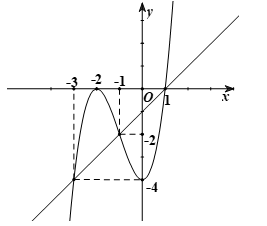
Khi đó: \(f'\left( x \right) = x - 1 \Leftrightarrow \left[ \begin{array}{l}x = - 3\\x = - 1\\x = 1\end{array} \right.\).
Bảng biến thiên của hàm số \(g\left( x \right)\).
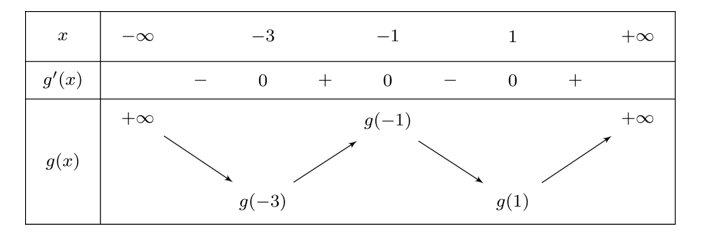
Ta có hàm số \(g\left( x \right)\) đồng biến trên khoảng \(\left( { - 3; - 1} \right)\) nên \(g\left( x \right)\) đồng biến trên khoảng \(\left( { - \frac{5}{2}; - \frac{3}{2}} \right)\).
Lời giải
Lợi nhuận doanh nghiệp thu được là \(h\left( x \right) = \left( {2000x - {x^2}} \right) - \left( {{x^2} + 1440x + 50} \right) - tx\)
\( = - 2{x^2} + \left( {560 - t} \right)x - 50\) với \(0 < x \le 2000\).
Xét hàm \(h\left( x \right) = - 2{x^2} + \left( {560 - t} \right)x - 50\) với \(0 < x \le 2000\).
Ta có \(h'\left( x \right) = - 4x + 560 - t = 0 \Rightarrow x = \frac{{560 - t}}{4} \in \left( {0;2000} \right)\).
Bảng biến thiên
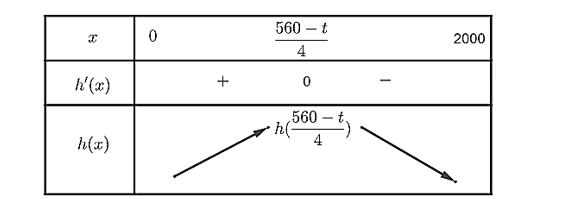
Từ bảng biến thiên ta thấy lợi nhuận doanh nghiệp cao nhất tại \(x = \frac{{560 - t}}{4}\).
Khi đó số tiền thuế thu được từ doanh nghiệp là \(k\left( t \right) = \frac{{560 - t}}{4}.t = - \frac{{{t^2}}}{4} + \frac{{560}}{4}t\) với \(0 < t < 300\).
Bảng biến thiên
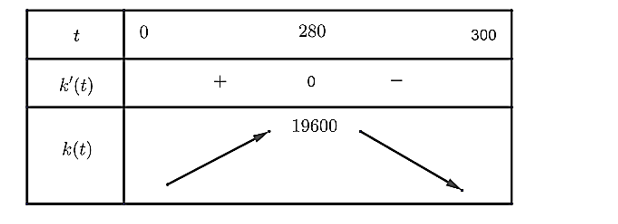
Từ bảng biến thiên ta thấy mức thuế phụ thu trên một đơn vị sản phẩm bán được là \(t = 280 \Rightarrow x = 70\) sản phẩm.
Vậy mức thuế phụ thu là 2800000 đồng/ sản phẩm, doanh nghiệp sản xuất và bán hết 70 sản phẩm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \(60^\circ \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
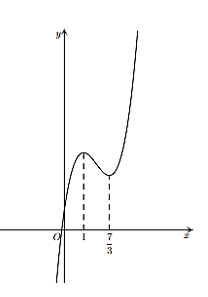
A. Hàm số nghịch biến trên khoảng \(\left( { - \infty ;1} \right)\).
B. Hàm số nghịch biến trên khoảng \(\left( { - \infty ;0} \right)\).
C. Hàm số nghịch biến trên khoảng \(\left( {\frac{7}{3}; + \infty } \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.