Cho hàm số \(y = \frac{{2x + m}}{{mx - 1}}\). Có bao nhiêu giá trị của \(m\)để đồ thị hàm số có tiệm cận đứng, tiệm cận ngang và các tiệm cận cùng với hai trục tọa độ tạo thành một hình chữ nhật có diện tích bằng 2.
Cho hàm số \(y = \frac{{2x + m}}{{mx - 1}}\). Có bao nhiêu giá trị của \(m\)để đồ thị hàm số có tiệm cận đứng, tiệm cận ngang và các tiệm cận cùng với hai trục tọa độ tạo thành một hình chữ nhật có diện tích bằng 2.
Quảng cáo
Trả lời:
Để đồ thị hàm số có tiệm cận đứng, tiệm cận ngang thì \(m \ne 0\).
Đồ thị hàm số có tiệm cận đứng là \(x = \frac{1}{m}\) và tiệm cận ngang là \(y = \frac{2}{m}\).
Vì diện tích bằng 2 nên \(\left| {\frac{1}{m}} \right|.\left| {\frac{2}{m}} \right| = 2 \Leftrightarrow m = \pm 1\).
Vậy có 2 giá trị của m.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) S, b) S, c) S, d) Đ
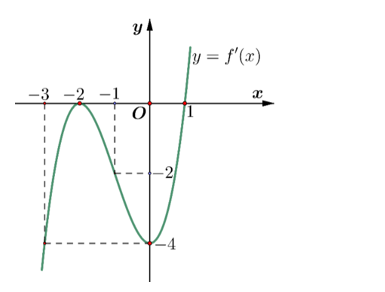
a) Vì từ đồ thị của hàm số \(y = f'\left( x \right)\) ta thấy \(f'\left( x \right) \ge 0\) với \(\forall x \ge 1\) nên hàm số đồng biến trên khoảng \(\left( {1; + \infty } \right)\).
b) Vì từ đồ thị của hàm số \(y = f'\left( x \right)\) ta thấy \(f'\left( x \right)\) chỉ đổi dấu một lần qua \(x = 1\) nên hàm số có một điểm cực trị.
c) Từ đồ thị ta có hàm số \(f'\left( x \right)\) có dạng: \(f'\left( x \right) = a{\left( {x + 2} \right)^2}\left( {x - 1} \right)\).
Đồ thị hàm số \(y = f'\left( x \right)\) đi qua \(\left( {0; - 4} \right)\) nên: \( - 4 = a{\left( {0 + 2} \right)^2}\left( {0 - 1} \right) \Leftrightarrow a = 1\).
Vậy \(f'\left( x \right) = {\left( {x + 2} \right)^2}\left( {x - 1} \right) \Rightarrow f'\left( 2 \right) = {\left( {2 + 2} \right)^2}\left( {2 - 1} \right) = 16\).
d) Ta có: \(g'\left( x \right) = f'\left( x \right) - x + 1 = 0 \Leftrightarrow f'\left( x \right) = x - 1\).
Vẽ đường thẳng \(y = x - 1\) trên cùng hệ trục tọa độ với đồ thị hàm số \(y = f'\left( x \right)\).
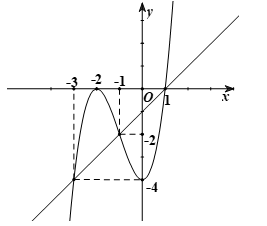
Khi đó: \(f'\left( x \right) = x - 1 \Leftrightarrow \left[ \begin{array}{l}x = - 3\\x = - 1\\x = 1\end{array} \right.\).
Bảng biến thiên của hàm số \(g\left( x \right)\).
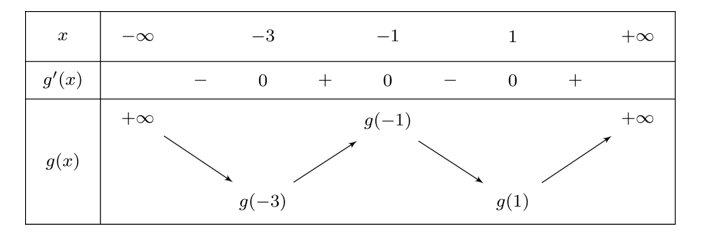
Ta có hàm số \(g\left( x \right)\) đồng biến trên khoảng \(\left( { - 3; - 1} \right)\) nên \(g\left( x \right)\) đồng biến trên khoảng \(\left( { - \frac{5}{2}; - \frac{3}{2}} \right)\).
Lời giải
Lợi nhuận doanh nghiệp thu được là \(h\left( x \right) = \left( {2000x - {x^2}} \right) - \left( {{x^2} + 1440x + 50} \right) - tx\)
\( = - 2{x^2} + \left( {560 - t} \right)x - 50\) với \(0 < x \le 2000\).
Xét hàm \(h\left( x \right) = - 2{x^2} + \left( {560 - t} \right)x - 50\) với \(0 < x \le 2000\).
Ta có \(h'\left( x \right) = - 4x + 560 - t = 0 \Rightarrow x = \frac{{560 - t}}{4} \in \left( {0;2000} \right)\).
Bảng biến thiên
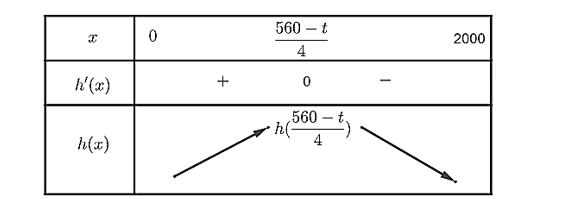
Từ bảng biến thiên ta thấy lợi nhuận doanh nghiệp cao nhất tại \(x = \frac{{560 - t}}{4}\).
Khi đó số tiền thuế thu được từ doanh nghiệp là \(k\left( t \right) = \frac{{560 - t}}{4}.t = - \frac{{{t^2}}}{4} + \frac{{560}}{4}t\) với \(0 < t < 300\).
Bảng biến thiên
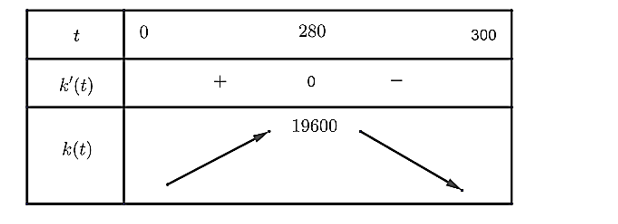
Từ bảng biến thiên ta thấy mức thuế phụ thu trên một đơn vị sản phẩm bán được là \(t = 280 \Rightarrow x = 70\) sản phẩm.
Vậy mức thuế phụ thu là 2800000 đồng/ sản phẩm, doanh nghiệp sản xuất và bán hết 70 sản phẩm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \(60^\circ \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
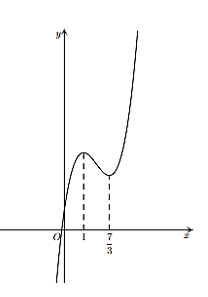
A. Hàm số nghịch biến trên khoảng \(\left( { - \infty ;1} \right)\).
B. Hàm số nghịch biến trên khoảng \(\left( { - \infty ;0} \right)\).
C. Hàm số nghịch biến trên khoảng \(\left( {\frac{7}{3}; + \infty } \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.