Câu hỏi:
11/02/2025 857
Cho các mệnh đề sau:
(I). Nếu một góc nhọn của tam giác vuông này bằng một góc nhọn của tam giác vuông kia thì hai tam giác vuông ấy đồng dạng.
(II). Nếu một cạnh góc vuông của tam giác vuông này bằng một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông ấy đồng dạng.
Khẳng định nào dưới đây là đúng?
Cho các mệnh đề sau:
(I). Nếu một góc nhọn của tam giác vuông này bằng một góc nhọn của tam giác vuông kia thì hai tam giác vuông ấy đồng dạng.
(II). Nếu một cạnh góc vuông của tam giác vuông này bằng một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông ấy đồng dạng.
Khẳng định nào dưới đây là đúng?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: A
Nếu một góc nhọn của tam giác vuông này bằng một góc nhọn của tam giác vuông kia thì hai tam giác vuông ấy đồng dạng.
Do đo mệnh đề (I) là đúng.
Mệnh đề (II) là sai vì khi sử dụng điều kiện về cạnh thì ta cần ít nhất hai cặp tỉ số cạnh bằng nhau.
Vậy chỉ có (I) đúng.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi quãng đường \(AB\) là \(x\) (\(x > 0\), km).
Thời gian xe tải đi hết quãng đường \(AB\) là \(\frac{x}{{30}}\) (giờ)
Ta có \(\frac{3}{4}\) quãng đường \(AB\) là \(\frac{3}{4}x\) (km), khi đó thời gian ô tô đi hết \(\frac{3}{4}\) quãng đường \(AB\) là:
\(\frac{3}{4}x:45 = \frac{x}{{60}}\) (giờ).
Vận tốc xe con sau khi tăng thêm \({\rm{5 km/h}}\) là: \(45 + 5 = 50\) (km/h).
Quãng đường còn lại là: \(1 - \frac{{3x}}{4} = \frac{x}{4}\) (km).
Thời gian xe con đi hết \(\frac{1}{4}\) quãng đường \(AB\) là \(\frac{x}{4}:50 = \frac{x}{{200}}\) (giờ)
Vì xe con đến \(B\) sớm hơn xe tải là 2 giờ 27 phút \(\left( { = \frac{{49}}{{20}}{\rm{ h}}} \right)\) nên ta có phương trình:
\(\frac{x}{{30}} - \left( {\frac{x}{{60}} + \frac{x}{{200}}} \right) = \frac{{49}}{{20}}\).
Giải phương trình, ta được:
\(\frac{x}{{30}} - \left( {\frac{x}{{60}} + \frac{x}{{200}}} \right) = \frac{{49}}{{20}}\)
\(\frac{{20x}}{{600}} - \left( {\frac{{10x}}{{600}} + \frac{{3x}}{{600}}} \right) = \frac{{1{\rm{ }}470}}{{600}}\)
\(\frac{{7x}}{{600}} = \frac{{1{\rm{ }}470}}{{600}}\)
\(7x = 1{\rm{ 470}}\)
\(x = 1{\rm{ 470:7}}\)
\(x = 210\) (thỏa mãn)
Vậy quãng đường \(AB\) dài \(210\)km.
Lời giải
Đáp án đúng là: a) Đ b) Đ c) S d) Đ
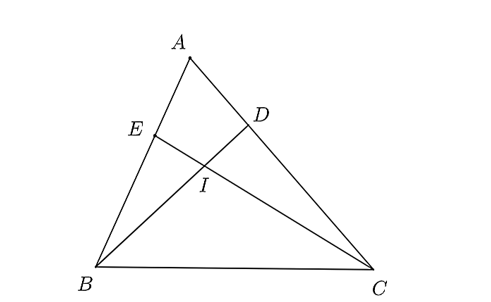
a) Theo đề, ta có nên \(\widehat {ADB} = \widehat {AEC}\) (hai góc tương ứng).
Do đó ý a) đúng.
b) Ta có: \(AC = 3AE\) hay \(\frac{{AE}}{{AC}} = \frac{1}{3}\); \(AD = \frac{1}{3}AB\) hay \(\frac{{AD}}{{AB}} = \frac{1}{3}\).
Suy ra \(\frac{{AE}}{{AC}} = \frac{{AD}}{{AB}} = \frac{1}{3}\). Do đó, ý b) đúng.
c) Xét \(\Delta ADE\) và \(\Delta ABC\), có:
\(\frac{{AE}}{{AC}} = \frac{{AD}}{{AB}} = \frac{1}{3}\) (cmt)
\(\widehat A\) chung (gt)
Do đó, (c.g.c)
Do đó, ý c) sai.
d) Vì nên \(\widehat {ABD} = \widehat {ACE}\) (2 góc tương ứng) (1)
Lại có, \(\widehat {EIB} = \widehat {DIC}\) (hai góc đối đỉnh) (2)
Từ (1) và (2) suy ra (g.g)
Suy ra \(\frac{{IE}}{{ID}} = \frac{{IB}}{{IC}}\) suy ra \(IE.IC = IB.ID\).
Do đó, ý d) đúng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
15 câu Trắc nghiệm Toán 8 Kết nối tri thức Bài 1: Đơn thức có đáp án
-
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
15 câu Trắc nghiệm Toán 8 Chân trời sáng tạo Bài 1: Đơn thức và đa thức nhiều biến có đáp án
-
Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 25
-
15 câu Trắc nghiệm Toán 8 Cánh diều Bài 1: Đơn thức nhiều biến. Đa thức nhiều biến có đáp án
-
Bộ 10 đề thi giữa kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 1
-
Đề cuối kì 2 Toán 8 Cánh diều cấu trúc mới có đáp án- Đề 2
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận