Cho biểu thức \(M = \frac{1}{{{x^3} - 2x}}.\left( {\frac{{{x^2} + 4}}{x} - 4} \right) + 1\) với \(x \ne 2\) và \(x \ne 0\). Tính giá trị của \(M\) biết \(\left| {4 - x} \right| = 2\).

Gọi quãng đường \(AB\) là \(x\) (\(x > 0\), km).

Thời gian xe tải đi hết quãng đường \(AB\) là \(\frac{x}{{30}}\) (giờ)

Ta có \(\frac{3}{4}\) quãng đường \(AB\) là \(\frac{3}{4}x\) (km), khi đó thời gian ô tô đi hết \(\frac{3}{4}\) quãng đường \(AB\) là:

\(\frac{3}{4}x:45 = \frac{x}{{60}}\) (giờ).

Vận tốc xe con sau khi tăng thêm \({\rm{5 km/h}}\) là: \(45 + 5 = 50\) (km/h).

Quãng đường còn lại là: \(1 - \frac{{3x}}{4} = \frac{x}{4}\) (km).

Thời gian xe con đi hết \(\frac{1}{4}\) quãng đường \(AB\) là \(\frac{x}{4}:50 = \frac{x}{{200}}\) (giờ)

Vì xe con đến \(B\) sớm hơn xe tải là 2 giờ 27 phút \(\left( { = \frac{{49}}{{20}}{\rm{ h}}} \right)\) nên ta có phương trình:

\(\frac{x}{{30}} - \left( {\frac{x}{{60}} + \frac{x}{{200}}} \right) = \frac{{49}}{{20}}\).

Giải phương trình, ta được:

\(\frac{x}{{30}} - \left( {\frac{x}{{60}} + \frac{x}{{200}}} \right) = \frac{{49}}{{20}}\)

\(\frac{{20x}}{{600}} - \left( {\frac{{10x}}{{600}} + \frac{{3x}}{{600}}} \right) = \frac{{1{\rm{ }}470}}{{600}}\)

\(\frac{{7x}}{{600}} = \frac{{1{\rm{ }}470}}{{600}}\)

\(7x = 1{\rm{ 470}}\)

\(x = 1{\rm{ 470:7}}\)

\(x = 210\) (thỏa mãn)

Vậy quãng đường \(AB\) dài \(210\)km.

Đáp án đúng là:                a) Đ         b) Đ         c) S         d) Đ

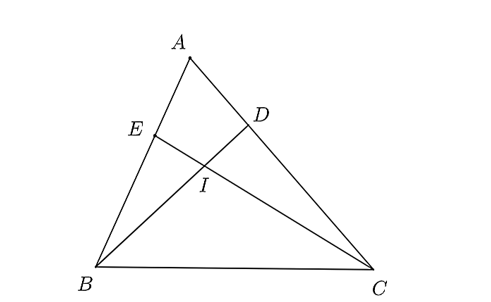
a) Theo đề, ta có  nên \(\widehat {ADB} = \widehat {AEC}\) (hai góc tương ứng).

Do đó ý a) đúng.

b) Ta có: \(AC = 3AE\) hay \(\frac{{AE}}{{AC}} = \frac{1}{3}\); \(AD = \frac{1}{3}AB\) hay \(\frac{{AD}}{{AB}} = \frac{1}{3}\).

Suy ra \(\frac{{AE}}{{AC}} = \frac{{AD}}{{AB}} = \frac{1}{3}\). Do đó, ý b) đúng.

c) Xét \(\Delta ADE\) và \(\Delta ABC\), có:

\(\frac{{AE}}{{AC}} = \frac{{AD}}{{AB}} = \frac{1}{3}\) (cmt)

\(\widehat A\) chung (gt)

Do đó,  (c.g.c)

Do đó, ý c) sai.

d) Vì  nên \(\widehat {ABD} = \widehat {ACE}\) (2 góc tương ứng) (1)

Lại có, \(\widehat {EIB} = \widehat {DIC}\) (hai góc đối đỉnh) (2)

Từ (1) và (2) suy ra  (g.g)

Suy ra \(\frac{{IE}}{{ID}} = \frac{{IB}}{{IC}}\) suy ra \(IE.IC = IB.ID\).

Do đó, ý d) đúng.