Cho \(\Delta ABC\) có đường trung tuyến \(AM\), đường phân giác của \(\widehat {AMB}\) cắt \(AB\) ở \(D\), đường phân giác của \(\widehat {AMC}\) cắt \(AC\) ở \(E\).
a) Chứng minh \(\frac{{AM}}{{BM}} = \frac{{AD}}{{BD}}\).
b) Chứng minh \(DE\parallel BC\) và \(AD.AC = AE.AB\).
c) Gọi \(I\) là trung điểm của \(DE\). Chứng minh ba điểm \(A,I,M\) thẳng hàng.
Cho \(\Delta ABC\) có đường trung tuyến \(AM\), đường phân giác của \(\widehat {AMB}\) cắt \(AB\) ở \(D\), đường phân giác của \(\widehat {AMC}\) cắt \(AC\) ở \(E\).
a) Chứng minh \(\frac{{AM}}{{BM}} = \frac{{AD}}{{BD}}\).
b) Chứng minh \(DE\parallel BC\) và \(AD.AC = AE.AB\).
c) Gọi \(I\) là trung điểm của \(DE\). Chứng minh ba điểm \(A,I,M\) thẳng hàng.
Câu hỏi trong đề: Bộ 5 đề thi giữa kì 2 Toán 8 Cánh diều cấu trúc mới có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
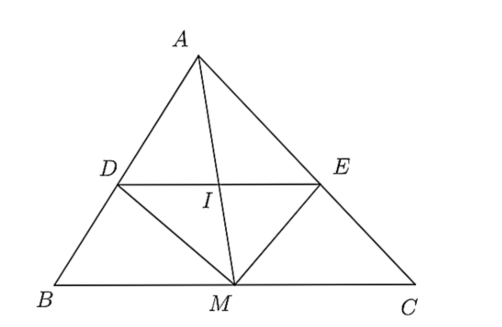
a) Xét \(\Delta ABM\) có \(MD\) là phân giác của \(\widehat {AMB}\) nên \(\frac{{AM}}{{BM}} = \frac{{AD}}{{BD}}\) (tính chất đường phân giác trong tam giác).
b) Xét \(\Delta AMC\) có \(ME\) là phân giác của \(\widehat {AMC}\) nên \(\frac{{AM}}{{BM}} = \frac{{AE}}{{CE}}\) (tính chất đường phân giác trong tam giác)
Từ phần a) ta có: \(\frac{{AM}}{{BM}} = \frac{{AD}}{{BD}}\) nên suy ra \(\frac{{AD}}{{BD}} = \frac{{AE}}{{CE}}\).
Do đó, \(DE\parallel BC\) (định lí Thalès đảo)
Ta có: \(\Delta ABC\) có \(DE\parallel BC\) nên theo định lí Thalès ta có: \(\frac{{AD}}{{AB}} = \frac{{AE}}{{AC}}\).
Suy ra \(AD.AC = AE.AB\) (đpcm).
c) Gọi \(I'\) là giao điểm của \(AM\) và \(DE\).
Ta có \(DI'\parallel BM\) suy ra \(\frac{{DI' & }}{{BM}} = \frac{{AI'}}{{AM}}\) (Hệ quả của định lí Thalès) (1)
\(EI'\parallel CM\) suy ra \(\frac{{EI' & }}{{CM}} = \frac{{AI'}}{{AM}}\) (Hệ quả của định lí Thalès) (2)
Từ (1) và (2) suy ra \(\frac{{DI' & }}{{BM}} = \frac{{EI'}}{{CM}}\) mà \(CM = BM\) (\(AM\) là đường trung tuyến của \(\Delta ABC\))
Suy ra \(DI' = EI'\).
Do đó \(I'\) trùng với \(I\).
Suy ra ba điểm \(A,I,M\) thẳng hàng.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
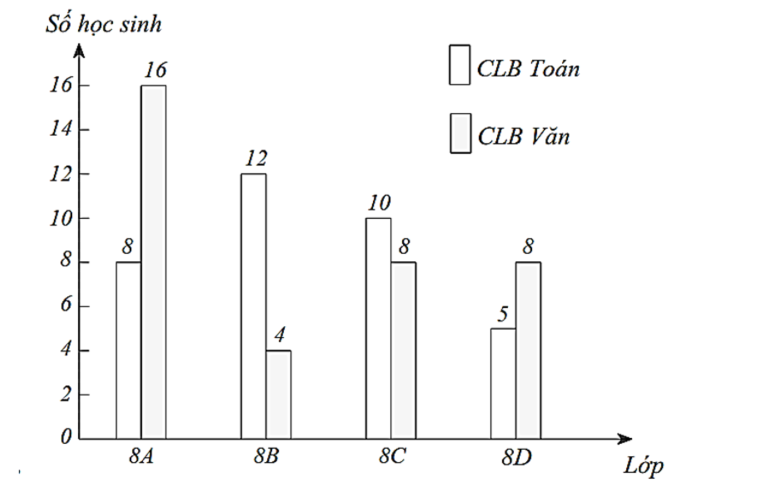
a) Ta có bảng thông kê sau:\(20\% \)
|
Lớp |
8A |
8B |
8C |
8D |
|
CLB Toán |
8 |
12 |
10 |
15 |
|
CLB Văn |
16 |
4 |
8 |
8 |
• Nhận thấy ở lớp 8A số lượng đăng kí câu lạc bộ Văn nhiều gấp 2 lần câu lạc bộ Toán. Trong khi đó, ở lớp 8B số học sinh tham gia câu lạc bộ Toán nhiều hơn câu lạc bộ Văn gấp 3 lần.
b) Lớp 8A có \(8\) bạn tham gia câu lạc bộ Toán chiếm tổng số học sinh cả lớp, nên lớp 8A có số học sinh là: \(8:20\% = 8:\frac{1}{5} = 40\) (học sinh).
Lớp 8A có \(8\) bạn tham gia câu lạc bộ Toán chiếm \(\frac{1}{{30}}\) số học sinh toàn khối nên số học sinh của toàn khối 8 đó là: \(8:\frac{1}{{30}} = 240\) (họ\(20\% \)c sinh).
Câu 2
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đáp án đúng là: A
Có 1 kết quả thuận lợi cho biến cố “Tấm thẻ được chọn ghi số \(5\)”.
Do đó, xác suất thực nghiệm của biến cố “Tấm thẻ được chọn ghi số \(5\)” là \(\frac{1}{4}.\)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \(20\% .\)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập